
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
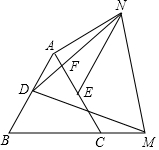 如图,等边△ABC中,AB=8,点D、E分别为AB、AC的中点,点M为射线BC上一动点,以DM为一边作等边△DMN.∠DAN=150°,DN交AE于F,线段NF的长为$\frac{2\sqrt{7}}{3}$.
如图,等边△ABC中,AB=8,点D、E分别为AB、AC的中点,点M为射线BC上一动点,以DM为一边作等边△DMN.∠DAN=150°,DN交AE于F,线段NF的长为$\frac{2\sqrt{7}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
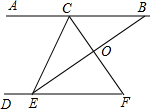 如图,点C、E分别在直线AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连结DF,再找出CF的中点O,然后连结EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.小华的想法对吗?为什么?
如图,点C、E分别在直线AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连结DF,再找出CF的中点O,然后连结EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.小华的想法对吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
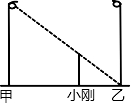 如图,甲、乙两盏路灯相距30米,一天晚上,当小刚从路灯甲底部向路灯乙底部直行25米时,发现自己的身影顶部正好接触到路灯乙的底部,已知小刚的身高为1.5米,那么路灯甲的高为( )
如图,甲、乙两盏路灯相距30米,一天晚上,当小刚从路灯甲底部向路灯乙底部直行25米时,发现自己的身影顶部正好接触到路灯乙的底部,已知小刚的身高为1.5米,那么路灯甲的高为( )| A. | 9米 | B. | 8米 | C. | 7米 | D. | 6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 cm | B. | 2.5 cm | C. | 3 cm | D. | 3.5 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
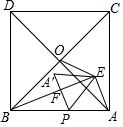 如图,在△ABE中,∠AEB=90°,AB=$\sqrt{29}$,以AB为边在△ABE的同侧作正方形ABCDD,点O是正方形对角线的交.点,连接OE,OE=$\frac{3}{2}$$\sqrt{2}$,点P为AB上一动点,将△APE沿直线PE翻折得到△A′PE,当A′P⊥BE于点F时,BF的长度是5-$\frac{10\sqrt{29}}{29}$.
如图,在△ABE中,∠AEB=90°,AB=$\sqrt{29}$,以AB为边在△ABE的同侧作正方形ABCDD,点O是正方形对角线的交.点,连接OE,OE=$\frac{3}{2}$$\sqrt{2}$,点P为AB上一动点,将△APE沿直线PE翻折得到△A′PE,当A′P⊥BE于点F时,BF的长度是5-$\frac{10\sqrt{29}}{29}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com