在一次消防演习中，消防员架起一架25米长的云梯AB，如图斜靠在一面墙上，梯子底端B离墙角C的距离为7米．
（1）求这个梯子的顶端距地面AC有多高？
（2）如果消防员接到命令，按要求将梯子底部在水平方向滑动后停在DE的位置上（云梯长度不变），测得BD长为8米，那么云梯的顶部在下滑了多少米？
【考点】勾股定理的应用．
【分析】（1）直接利用勾股定理求得直角边AC的长即可；
（2）首先求得CD的长，然后利用勾股定理求得线段EC的长，最后求得线段AE的长即可．
【解答】解：（1）由图可以看出梯子墙地可围成一个直角三角形，
即梯子为斜边，梯子底部到墙的距离线段为一个直角边，梯子顶端到地的距离线段为另一个直角边，
所以梯子顶端到地的距离为252﹣72=242，所以梯子顶端到地为24米．
（2）当梯子顶端下降4米后，梯子底部到墙的距离变为252﹣（24﹣4）2=152，
15﹣7=8所以，梯子底部水平滑动8米即可．
【点评】此题为利用勾股定理解直角三角形问题，会利用勾股定理即可，难度适中．
名校课堂系列答案科目：初中数学 来源： 题型：
Rt△ABC与Rt△FED是两块全等的含30°、60°角的三角板，按如图（一）所示拼在一起，CB与DE重合．
（1）求证：四边形ABFC为平行四边形；
（2）取BC中点O，将△ABC绕点O顺时钟方向旋转到如图（二）中△A′B′C′位置，直线B'C'与AB、CF分别相交于P、Q两点，猜想OQ、OP长度的大小关系，并证明你的猜想；
（3）在（2）的条件下，指出当旋转角至少为多少度时，四边形PCQB为菱形？（不要求证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
阅读材料：
小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+
=（1+
）2．善于思考的小明进行了以下探索：
设a+b
=（m+n）2（其中a、b、m、n均为整数），则有a+b=m2+2n2+2mn．
∴a=m2+2n2，b=2mn．这样小明就找到了一种把类似a+b的式子化为平方式的方法．
请你仿照小明的方法探索并解决下列问题：
（1）当a、b、m、n均为正整数时，若a+b
=
，用含m、n的式子分别表示a、b，得：a= ，b= ；
（2）利用所探索的结论，找一组正整数a、b、m、n填空： + =（ + 
）2；
（3）若a+4=，且a、m、n均为正整数，求a的值？
查看答案和解析>>
科目：初中数学 来源： 题型：
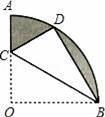
如图，在扇形AOB中，∠AOB=90°，半径OA=6，将扇形AOB沿过点B的直线折叠，点O恰好落在弧AB上点D处，折痕交OA于点C，整个阴影部分的面积 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
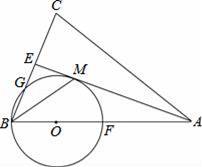
如图，在△ABC中，AB=AC，AE是∠BAC的平分线，∠ABC的平分线 BM交AE于点M，点O在AB上，以点O为圆心，OB的长为半径的圆经过点M，交BC于点G，交 AB于点F．
（1）求证：AE为⊙O的切线．
（2）当BC=8，AC=12时，求⊙O的半径．
（3）在（2）的条件下，求线段BG的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
B．
D．
