
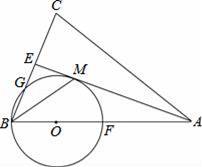
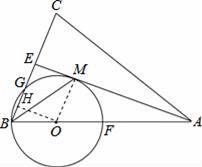
如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.

【考点】圆的综合题.
【专题】证明题.
【分析】(1)连接OM.利用角平分线的性质和平行线的性质得到AE⊥OM后即可证得AE是⊙O的切线;
(2)设⊙O的半径为R,根据OM∥BE,得到△OMA∽△BEA,利用平行线的性质得到
 =
=
 ,即可解得R=3,从而求得⊙O的半径为3;
,即可解得R=3,从而求得⊙O的半径为3;
(3)过点O作OH⊥BG于点H,则BG=2BH,根据∠OME=∠MEH=∠EHO=90°,得到四边形OMEH是矩形,从而得到HE=OM=3和BH=1,证得结论BG=2BH=2.
【解答】(1)证明:连接OM.
∵AC=AB,AE平分∠BAC,
∴AE⊥BC,CE=BE=
 BC=4,
BC=4,
∵OB=OM,
∴∠OBM=∠OMB,
∵BM平分∠ABC,
∴∠OBM=∠CBM,
∴∠OMB=∠CBM,
∴OM∥BC
又∵AE⊥BC,
∴AE⊥OM,
∴AE是⊙O的切线;
(2)设⊙O的半径为R,
∵OM∥BE,
∴△OMA∽△BEA,
∴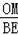
 =
=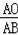
 即
即
 =
=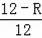
 ,
,
解得R=3,
∴⊙O的半径为3;
(3)过点O作OH⊥BG于点H,则BG=2BH,
∵∠OME=∠MEH=∠EHO=90°,
∴四边形OMEH是矩形,
∴HE=OM=3,
∴BH=1,
∴BG=2BH=2.

【点评】本题考查了圆的综合知识,题目中还运用到了切线的判定与性质、相似三角形的判定与性质,综合性较强,难度较大.


科目:初中数学 来源: 题型:
在一次消防演习中,消防员架起一架25米长的云梯AB,如图斜靠在一面墙上,梯子底端B离墙角C的距离为7米.
(1)求这个梯子的顶端距地面AC有多高?
(2)如果消防员接到命令,按要求将梯子底部在水平方向滑动后停在DE的位置上(云梯长度不变),测得BD长为8米,那么云梯的顶部在下滑了多少米?


查看答案和解析>>
科目:初中数学 来源: 题型:
国务院总理李克强在第十二届全国人大第四次政府工作报告中指出,2015年我国国内生产总值达到了67.7万亿元,67.7万亿元用科学记数法表示为( )
A.67.7×1012 B.6.77×1013 C.0.677×1014 D.6.77×1014
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中逆命题是真命题的是( )
A.对顶角相等
B.若两个角都是45°,那么这两个角相等
C.全等三角形的对应角相等
D.两直线平行,同位角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
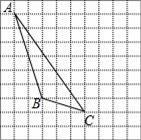
如图,在方格纸内将△ABC水平向右平移5个单位得到△A′B′C′.
(1)补全△A′B′C′;利用网格点和直尺画图:
(2)画出AB边上的高线CD;
(3)图中△ABC的面积是 ;
(4)△ABC与△EBC面积相等,在图中描出所有满足条件且异于A点的格点E,并记为E1E2E3.

查看答案和解析>>
科目:初中数学 来源: 题型:
甲乙两车沿直路同向行驶,车速分别为20m/s和25m/s.现甲车在乙车前500m处,设xs(0≤x≤100)后两车相距ym.那么y关于x的数解析式为 .(写出自变量取值范围)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com