练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

     如图，AB∥CD，AD平分∠BAC，若∠BAD=70°，那么∠ACD的度数为（　　）

    A．40°   B．35°    C．50°   D．45°


    A【考点】平行线的性质．

    【分析】根据角平分线定义求出∠BAC，根据平行线性质得出∠ACD+∠BAC=180°，代入求出即可．

    【解答】解：∵AD平分∠BAC，∠BAD=70°，

    ∴∠BAC=2∠BAD=140°，

    ∵AB∥CD，

    ∴∠ACD=180°﹣∠BAC=40°，

    故选：A．

    【点评】本题考查了角平分线定义和平行线的性质的应用，关键是求出∠BAC的度数，再结合∠ACD+∠BAC=180°．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    Rt△ABC与Rt△FED是两块全等的含30°、60°角的三角板，按如图（一）所示拼在一起，CB与DE重合．

    （1）求证：四边形ABFC为平行四边形；

    （2）取BC中点O，将△ABC绕点O顺时钟方向旋转到如图（二）中△A′B′C′位置，直线B'C'与AB、CF分别相交于P、Q两点，猜想OQ、OP长度的大小关系，并证明你的猜想；

    （3）在（2）的条件下，指出当旋转角至少为多少度时，四边形PCQB为菱形？（不要求证明）

    　


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是（　　）

    ①∠DCF=∠BCD；②EF=CF；③S△BEC=2S△CEF；④∠DFE=3∠AEF．

    A．①② B．②③④     C．①②④     D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．如图是小李销售某种食品的总利润y元与销售量x千克的函数图象（总利润=总销售额﹣总成本）．由于目前销售不佳，小李想了两个解决方案：

    方案（1）是不改变食品售价，减少总成本；

    方案（2）是不改变总成本，提高食品售价．

    下面给出的四个图象中虚线表示新的销售方式中利润与销售量的函数图象，则分别反映了方案（1）（2）的图象是（　　）

    A．②，③     B．①，③     C．①，④     D．④，②

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，四边形ABCD是⊙O的内接四边形，若∠BOD=88°，则∠BCD的度数是（　　）

    A．88°   B．92°    C．106°  D．136°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


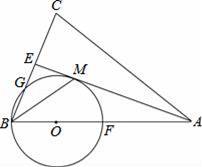
    如图，在△ABC中，AB=AC，AE是∠BAC的平分线，∠ABC的平分线 BM交AE于点M，点O在AB上，以点O为圆心，OB的长为半径的圆经过点M，交BC于点G，交 AB于点F．

    （1）求证：AE为⊙O的切线．

    （2）当BC=8，AC=12时，求⊙O的半径．

    （3）在（2）的条件下，求线段BG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，∠AOB=30°，点M、N分别在边OA、OB上，且OM=1，ON=3，点P、Q分别在边OB、OA上，则MP+PQ+QN的最小值是　　　　　　．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ﹣5的绝对值是（　　）

    A．5       B．﹣5   C．      D．﹣

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，∠B=∠C=67.5°．

    （Ⅰ）求sinA的值；

    （Ⅱ）求tanC的值．

    查看答案和解析>>

    同步练习册答案