
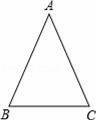
如图,在△ABC中,∠B=∠C=67.5°.
(Ⅰ)求sinA的值;
(Ⅱ)求tanC的值.

【考点】解直角三角形.
【专题】探究型.
【分析】(1)要求sinA的值,根据三角形内角和可求得∠A的度数,从而可以求得sinA的值;
(2)要求tanC的值,只要作辅助线BD⊥AC于点D,然后通过变形,即可求得tanC的值.
【解答】解:(1)∵在△ABC中,∠B=∠C=67.5°,
∴∠A=180°﹣∠B﹣∠C=180°﹣67.5°﹣67.5°=45°,
∴sinA=sin45°=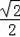
 ,
,
即sinA=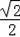
 ;
;
(2)作BD⊥AC于点D,如下图所示,
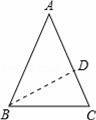

∵由(1)可知∠A=45°,设BD=a,
∴AD=a,AB=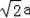
 ,
,
∵AB=AC,
∴AC=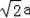
 ,
,
∴CD=AC﹣AD=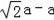
 ,
,
∴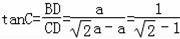
 =
=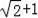
 ,
,
即tanC=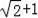
 .
.
【点评】本题考查解直角三角形、三角形的内角和、求角的三角函数值,解题的关键是明确题意,找出对应量,求出相应的三角函数值.


科目:初中数学 来源: 题型:
下列各式中,不能用平方差公式计算的是( )
A.(﹣x﹣y)(x﹣y) B.(﹣x+y)(﹣x﹣y) C.(x+y)(﹣x+y) D.(x﹣y)(﹣x+y)
查看答案和解析>>
科目:初中数学 来源: 题型:
.数学活动课上,老师提出这样一个问题:如果AB=BC,∠ABC=60°,∠APC=30°,连接PB,那么PA、PB、PC之间会有怎样的等量关系呢?经过思考后,部分同学进行了如下的交流:
小蕾:我将图形进行了特殊化,让点P在BA延长线上(如图1),得到了一个猜想:PA2+PC2=PB2.
小东:我假设点P在∠ABC的内部,根据题目条件,这个图形具有“共端点等线段”的特点,可以利用旋转解决问题,旋转△PAB后得到△P′CB,并且可推出△PBP′,△PCP′分别是等边三角形、直角三角形,就能得到猜想和证明方法.
这时老师对同学们说,请大家完成以下问题:
(1)如图2,点P在∠ABC的内部,
①PA=4,PC=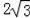
 ,PB= .
,PB= .
②用等式表示PA、PB、PC之间的数量关系,并证明.
(2)对于点P的其他位置,是否始终具有②中的结论?若是,请证明;若不是,请举例说明.
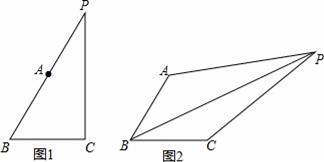

查看答案和解析>>
科目:初中数学 来源: 题型:
甲乙两车沿直路同向行驶,车速分别为20m/s和25m/s.现甲车在乙车前500m处,设xs(0≤x≤100)后两车相距ym.那么y关于x的数解析式为 .(写出自变量取值范围)
查看答案和解析>>
科目:初中数学 来源: 题型:
随着人们生活质量的提高,观光旅游已经成为人们休闲度假的一种方式.“清明小长假”将至,旅游部门随机电话访谈若干名市民,调查了解他们小长假期间选择外出游玩的类型:近郊游、国内长线游、出国游和其他.根据电话访谈的结果制成统计图,根据没有制作完成的统计图提供的信息回答下列问题.
(1)选择其他方式的人数是多少?
(2)补全条形统计图和扇形统计图;
(3)若A,B在 4月3号在①“西岭雪山”、②安仁古镇和③新场古镇三个地方中选择其中的一地方游玩.(三个景点被A和B选中的可能性相同).用树状图或者列表法写出A,B两人选择的所有可能结果,并求A,B两人选择在不同地方游玩的概率.(树状图或者列表可以直接用每个景点前的数字番号即可)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com