
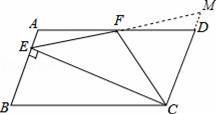
如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )
①∠DCF=
 ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.


A.①② B.②③④ C.①②④ D.①②③④
C【考点】平行四边形的性质;全等三角形的判定与性质;直角三角形斜边上的中线.
【分析】由在平行四边形ABCD中,AD=2AB,F是AD的中点,易得AF=FD=CD,继而证得①∠DCF=
 ∠BCD;然后延长EF,交CD延长线于M,分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF(ASA),得出对应线段之间关系进而得出答案.
∠BCD;然后延长EF,交CD延长线于M,分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF(ASA),得出对应线段之间关系进而得出答案.
【解答】解:①∵F是AD的中点,
∴AF=FD,
∵在▱ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=
 ∠BCD,故此选项正确;
∠BCD,故此选项正确;
②延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
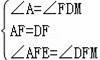
 ,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FM,故②正确;
③∵EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
④设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°﹣x,
∴∠EFC=180°﹣2x,
∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x,
∵∠AEF=90°﹣x,
∴∠DFE=3∠AEF,故此选项正确.
故选C.

【点评】此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,得出△AEF≌△DME是解题关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和
30°,
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果精确到1m)


查看答案和解析>>
科目:初中数学 来源: 题型:
国务院总理李克强在第十二届全国人大第四次政府工作报告中指出,2015年我国国内生产总值达到了67.7万亿元,67.7万亿元用科学记数法表示为( )
A.67.7×1012 B.6.77×1013 C.0.677×1014 D.6.77×1014
查看答案和解析>>
科目:初中数学 来源: 题型:
定义新运算:对于任意实数a,b(其中a≠0),都有a⊗b=
 ,等式右边是通常的加法、减法及除法运算,比如:2⊗1=
,等式右边是通常的加法、减法及除法运算,比如:2⊗1=
 =0
=0
(1)求5⊗4的值;
(2)若x⊗2=1(其中x≠0),求x的值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com