
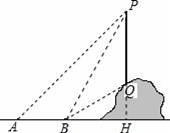
如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和
30°,
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果精确到1m)


【考点】解直角三角形的应用-仰角俯角问题.
【分析】(1)作PQ⊥AB交AB的延长线于H,根据三角形的外角的性质计算;
(2)设PQ=xm,根据正、余弦的定义表示出QH、BH,根据等腰直角三角形的性质列式计算即可.
【解答】解:(1)作PQ⊥AB交AB的延长线于H,
由题意得,∠QBH=30°,∠PBH=60°,
∴∠BQH=60°,∠PBQ=30°,
∴∠BPQ=∠BQH﹣∠PBQ=30°;
(2)设PQ=xm,
∵∠BPQ=∠PBQ,
∴BQ=PQ=xm,
∵∠QBH=30°,
∴QH=
 BQ=
BQ=
 x,BH=
x,BH=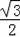
 x,
x,
∵∠A=45°,
∴6+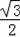
 x=x
x=x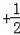
 x,
x,
解得x=2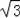
 +6≈9.
+6≈9.
答:该电线杆PQ的高度约为9m.

【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.


科目:初中数学 来源: 题型:
如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24m,MG=8m,MC=6m,则阴影部分地的面积是( )m2.


A.168 B.128 C.98 D.156
查看答案和解析>>
科目:初中数学 来源: 题型:
Rt△ABC与Rt△FED是两块全等的含30°、60°角的三角板,按如图(一)所示拼在一起,CB与DE重合.
(1)求证:四边形ABFC为平行四边形;
(2)取BC中点O,将△ABC绕点O顺时钟方向旋转到如图(二)中△A′B′C′位置,直线B'C'与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想;
(3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形?(不要求证明)


查看答案和解析>>
科目:初中数学 来源: 题型:
利用基本尺规作图,下列条件中,不能作出唯一直角三角形的是( )
A.已知斜边和一锐角 B.已知一直角边和一锐角
C.已知斜边和一直角边 D.已知两个锐角
查看答案和解析>>
科目:初中数学 来源: 题型:
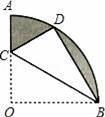
如图,在扇形AOB中,∠AOB=90°,半径OA=6,将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,整个阴影部分的面积 .

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )
①∠DCF=
 ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.


A.①② B.②③④ C.①②④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图是小李销售某种食品的总利润y元与销售量x千克的函数图象(总利润=总销售额﹣总成本).由于目前销售不佳,小李想了两个解决方案:
方案(1)是不改变食品售价,减少总成本;
方案(2)是不改变总成本,提高食品售价.
下面给出的四个图象中虚线表示新的销售方式中利润与销售量的函数图象,则分别反映了方案(1)(2)的图象是( )


A.②,③ B.①,③ C.①,④ D.④,②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com