
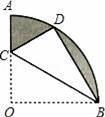
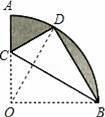
如图,在扇形AOB中,∠AOB=90°,半径OA=6,将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,整个阴影部分的面积 .

9π﹣12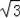
 .
.
【考点】翻折变换(折叠问题);扇形面积的计算.
【分析】首先连接OD,由折叠的性质,可得CD=CO,BD=BO,∠DBC=∠OBC,则可得△OBD是等边三角形,继而求得OC的长,即可求得△OBC与△BCD的面积,又在扇形OAB中,∠AOB=90°,半径OA=6,即可求得扇形OAB的面积,继而求得阴影部分面积.
【解答】解:连接OD.
根据折叠的性质,CD=CO,BD=BO,∠DBC=∠OBC,
∴OB=OD=BD,
即△OBD是等边三角形,
∴∠DBO=60°,
∴∠CBO=
 ∠DBO=30°,
∠DBO=30°,
∵∠AOB=90°,
∴OC=OB•tan∠CBO=6×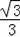
 =2
=2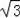
 ,
,
∴S△BDC=S△OBC=
 ×OB×OC=
×OB×OC=
 ×6×2
×6×2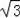
 =6
=6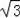
 ,S扇形AOB=
,S扇形AOB=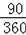
 π×62=9π,
π×62=9π,
∴整个阴影部分的面积为:S扇形AOB﹣S△BDC﹣S△OBC=9π﹣6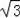
 ﹣6
﹣6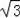
 =9π﹣12
=9π﹣12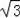
 .
.
故答案为:9π﹣12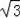
 .
.

【点评】此题考查了折叠的性质、扇形面积公式以及直角三角形的性质.此题难度适中,注意数形结合思想的应用,注意辅助线的作法.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
在一次消防演习中,消防员架起一架25米长的云梯AB,如图斜靠在一面墙上,梯子底端B离墙角C的距离为7米.
(1)求这个梯子的顶端距地面AC有多高?
(2)如果消防员接到命令,按要求将梯子底部在水平方向滑动后停在DE的位置上(云梯长度不变),测得BD长为8米,那么云梯的顶部在下滑了多少米?


查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法正确的是( )
A.对角线相等的平行四边形是菱形
B.有一组邻边相等的平行四边形是菱形
C.对角线相互垂直的四边形是菱形
D.有一个角是直角的平行四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和
30°,
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果精确到1m)


查看答案和解析>>
科目:初中数学 来源: 题型:
国务院总理李克强在第十二届全国人大第四次政府工作报告中指出,2015年我国国内生产总值达到了67.7万亿元,67.7万亿元用科学记数法表示为( )
A.67.7×1012 B.6.77×1013 C.0.677×1014 D.6.77×1014
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中逆命题是真命题的是( )
A.对顶角相等
B.若两个角都是45°,那么这两个角相等
C.全等三角形的对应角相等
D.两直线平行,同位角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
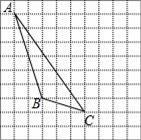
如图,在方格纸内将△ABC水平向右平移5个单位得到△A′B′C′.
(1)补全△A′B′C′;利用网格点和直尺画图:
(2)画出AB边上的高线CD;
(3)图中△ABC的面积是 ;
(4)△ABC与△EBC面积相等,在图中描出所有满足条件且异于A点的格点E,并记为E1E2E3.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com