
 ��ͼ���ڡ�ABC�У���C=90�㣬AC=BC=4��DΪAC�е㣬MΪ�߶�AB��һ���㣨M����A��B�غϣ�������M��BC��ƽ���߽�BD�ڵ�N����MNΪ�Խ�����������MPNQ����MN�ij�Ϊm��
��ͼ���ڡ�ABC�У���C=90�㣬AC=BC=4��DΪAC�е㣬MΪ�߶�AB��һ���㣨M����A��B�غϣ�������M��BC��ƽ���߽�BD�ڵ�N����MNΪ�Խ�����������MPNQ����MN�ij�Ϊm������ ��1�����������ε�������ڶԽ��߳˻���һ�뼴�ɽ�����⣮
��2����ͼ1�У���NH��BC���Ƴ�$\frac{NH}{BC}$=$\frac{DH}{CD}$���õ�$\frac{NH}{DH}$=$\frac{BC}{CD}$=2����DH=$\frac{1}{2}$NH=$\frac{1}{4}$m������HM=AH���г����̼��ɽ�����⣮
��3���������������ۼ��ɣ��ٵ�0��m��2ʱ��S=$\frac{1}{2}$m2���ڵ�2��m��$\frac{8}{3}$ʱ����ͼ3�У��ص������������MPEFQ���۵�$\frac{8}{3}$��m��4ʱ����ͼ4�У��ص������ǡ�MEA���ֱ����������ɣ�
��4�����������г����̼��ɽ�����⣮
��� �⣺��1�����ı���MPNA�������Σ�
��S������ABCD=$\frac{1}{2}$•MN2=$\frac{{m}^{2}}{2}$��
��2����ͼ1�У�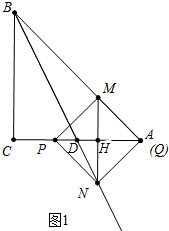
��NH��BC��
��$\frac{NH}{BC}$=$\frac{DH}{CD}$��
��$\frac{NH}{DH}$=$\frac{BC}{CD}$=2��
��DH=$\frac{1}{2}$NH=$\frac{1}{4}$m��
��HM=AH��
��$\frac{1}{2}$m=2-$\frac{1}{4}$m��
��m=$\frac{8}{3}$��
��3����ͼ2�У�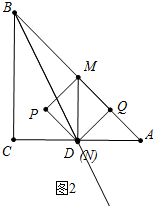
��D��N�غ�ʱ��DM=AD=2��m=2��
�൱0��m��2ʱ��S=$\frac{1}{2}$m2��
��2��m��$\frac{8}{3}$ʱ����ͼ3�У��ص������������MPEFQ��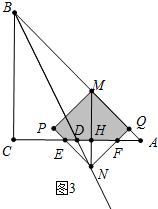
��NH=x����DH=$\frac{1}{2}$x��
��HM=HA��
��m-x=2-$\frac{1}{2}$x��
��x=2m-4��
��S=$\frac{1}{2}$m2-$\frac{1}{2}$•2��2m-4��•��2m-4��=��2m-4��2��
��$\frac{8}{3}$��m��4ʱ����ͼ4�У�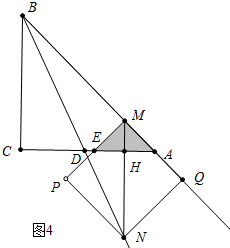
��NH=2m-4��
��MH=m-��2m-4��=4-m��
��S=$\frac{1}{2}$��2��4-m��•��4-m��=��4-m��2��
��������S=$\left\{\begin{array}{l}{\frac{1}{2}{m}^{2}}&{��0��m��2��}\\{��2m-4��^{2}}&{��2��m��\frac{8}{3}��}\\{��4-m��^{2}}&{��\frac{8}{3}��m��4��}\end{array}\right.$��
��4���������֪��4-$\frac{1}{2}$m-��4-m��=4-2m ��4-$\frac{1}{2}$m-��4-m��=2m-4��
���m=$\frac{8}{5}$��$\frac{8}{3}$��
���� ���⿼���ı����ۺ��⡢����ֱ�������ε����ʡ������ε����ʵ�֪ʶ������Ĺؼ���ѧ��������ۣ�ѧ�ử��ͼ�ν�����⣬������ת��Ϊ����ȥ˼���������п�ѹ���⣮


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com