
【题目】如图,等腰直角![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() .
.

(1)求证:![]() ;
;
(2)若![]() 的外角平分线以及
的外角平分线以及![]() 的平分线交于点
的平分线交于点![]() ,(1)结论是否成立?请在图中补全图形,写出结论,并说明理由.
,(1)结论是否成立?请在图中补全图形,写出结论,并说明理由.
【答案】(1)见解析;(2)不成立,![]() ,理由见解析
,理由见解析
【解析】
(1)根据三角形的内角和定理,得出∠PAB+∠PBA=45°,∠PCB+∠PBC=67.5°,即可求出∠APB=135°,∠BPC=112.5°,作辅助线在AB上截取BG=BC,可证出△PBC≌△PBG(SAS),即可得出∠BPC=∠BPG=112.5°,PC=PG,BC=BG,再可证出∠APG=∠APB-∠BPG=22.5°,得出∠PAG=∠APG,进而得出AG=PG,即可得出AB=CP+BC.
(2)(1)中的结论不成立;延长AB至G,使BG=BC,先证得∠ACG=∠CBP112.5°,∠CAB=∠PCB=45°,然后根据ASA证得△GAC≌△PCB,即可证得PC=AB+BC.
(1)证明:在AB上截取BG=BC,
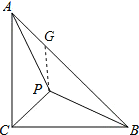
∵等腰Rt△ABC中,AC=BC,∠ACB=90°,
∴∠BAC=∠ABC=45°,
∵∠A、∠B、∠C的平分线交于点P.
∴∠PAB=∠PBA=22.5°,∠ACP=∠BCP=45°,
∴∠PAB+∠PBA=45°,∠PCB+∠PBC=67.5°
∴∠APB=135°,∠BPC=112.5°,
在△PBC和△PBG中,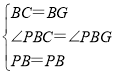 ,
,
∴△PBC≌△PBG(SAS),
∴∠BPC=∠BPG=112.5°,PC=PG,BC=BG,
∴∠APG=∠APB-∠BPG=22.5°,
∴∠PAG=∠APG,
∴AG=PG,
∴AG=PC,
∴AB=BG+AG=CP+BC,
即AB=CP+BC;
(2)不成立,
如图2所示,PC=AB+BC;
证明:延长AB至G,使BG=BC,
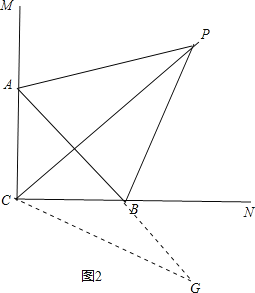
∴∠BCG=∠BGC,
∵∠CAB=∠ABC=45°,
∴∠CBG=135°,
∴∠BCG=∠BGC=22.5°,
∴∠ACG=112,5°,
∵∠A、∠B的外角平分线以及∠C的平分线交于点P,
∴∠PCB=45°,∠PBC=112.5°,
∴∠ACG=∠CBP,∠CAB=∠PCB=45°,
在△GAC和△PCB中,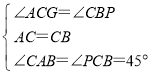 ,
,
∴△GAC≌△PCB(ASA),
∴AG=CP,
∴CP=AB+BG=AB+CB,
结论:![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于![]() MN长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( )
MN长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( )
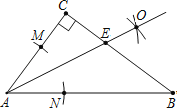
A.8B.7C.6D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
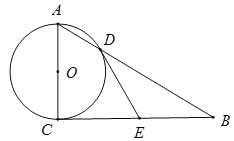
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系:_________;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC=_______时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
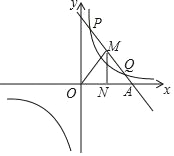
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)直接写出不等式k1x+b≥![]() 的解集;
的解集;
(3)M为线段PQ上一点,且MN⊥x轴于N,求△MON的面积最大值及对应的M点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
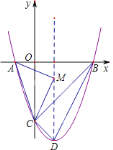
【题目】如图所示:抛物线![]() 交坐标轴于
交坐标轴于![]() 、
、![]() 、
、![]() 三点,
三点,![]() 是抛物线的顶点,
是抛物线的顶点,![]() 在对称轴上,
在对称轴上,![]() 在坐标轴上.以下结论:
在坐标轴上.以下结论:
①存在点![]() ,使
,使![]() 是等腰直角三角形;②
是等腰直角三角形;②![]() 的最小值是
的最小值是![]() ;③
;③![]() 的最大值是
的最大值是![]() ;④若
;④若![]() 与
与![]() 相似,则
相似,则![]() 的坐标恰有两个.
的坐标恰有两个.
其中正确的是________(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.

(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,在△ ABC中,∠ACB = 2∠B, ∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥ AO于H,分别交直线AB、AC、BC于点N、E、M
(1)当直线l经过点C时(如图 2),求证:NH = CH;
(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;
(3)请直接写出BN、CE、CD之间的等量关系.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)△ABC的面积为__________;
(2)在图中作出△ABC关于直线MN的对称图形△A′B′C′.
(3)利用网格纸,在MN上找一点P,使得PB+PC的距离最短.( 保留痕迹)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com