
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)直接写出不等式k1x+b≥![]() 的解集;
的解集;
(3)M为线段PQ上一点,且MN⊥x轴于N,求△MON的面积最大值及对应的M点坐标.
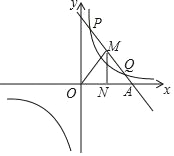
【答案】(1)y=![]() ,y=﹣2x+9;(2)当x<0或
,y=﹣2x+9;(2)当x<0或![]() <x<4时,k1x+b≥
<x<4时,k1x+b≥![]() ;(3)当x=
;(3)当x=![]() 时,面积最大值为
时,面积最大值为![]() ,M(
,M(![]() ,
,![]() )
)
【解析】
(1)首先把P(![]() ,8)代入反比例函数解析式中确定k2的值,得到反比例函数解析式;然后把Q(4,m)代入反比例函数确定m的值,再根据P,Q两点坐标利用待定系数法确定一次函数解析式;
,8)代入反比例函数解析式中确定k2的值,得到反比例函数解析式;然后把Q(4,m)代入反比例函数确定m的值,再根据P,Q两点坐标利用待定系数法确定一次函数解析式;
(2)根据函数的图象即可求得;
(3)设M(x,﹣2x+9),则ON=x,MN=﹣2X+9,根据三角形面积公式即可得到关于x的二次函数,将其化为顶点式,即可得到函数的最大值,从而确定M点的坐标.
(1)∵点P(![]() ,8)在反比例函数图象上,
,8)在反比例函数图象上,
∴8=![]() ,
,
∴k2=4,
∴反比例函数的表达式为:![]() ,
,
∵Q(4,m)在反比例函数的图象上,
∴m=![]() =1,
=1,
∴Q(4,1),
把P(![]() ,8),Q(4,1)分别代入一次函数y=k1x+b中,
,8),Q(4,1)分别代入一次函数y=k1x+b中,
∴![]() ,
,![]() ,
,
解得:k1=-2,b=9,
∴一次函数的表达式为y=﹣2x+9;
即反比例函数的表达式:![]() ,一次函数的表达式为:y=﹣2x+9;
,一次函数的表达式为:y=﹣2x+9;
(2)由图象得:当x<0或![]() <x<4时,k1x+b≥
<x<4时,k1x+b≥![]() .
.
(3)设M(x,﹣2x+9),
∴ON=x,MN=﹣2X+9,
∴S△MON=![]() ×ON×MN=
×ON×MN=![]() x×(﹣2x+9)=﹣x2+
x×(﹣2x+9)=﹣x2+![]() x=﹣(x﹣
x=﹣(x﹣![]() )2+
)2+![]() ,
,
∴当x=![]() 时,面积最大值为
时,面积最大值为![]() ,
,
即M(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 与等腰
与等腰![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 和
和![]() 相交于点
相交于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 与点
与点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④若
;④若![]() ,则
,则![]() .其中一定正确的结论的个数是( )
.其中一定正确的结论的个数是( )
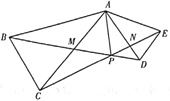
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,以大于![]() EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )

A. 120° B. 30° C. 150° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地开往B地,甲车比乙车早出发2小时,并且在途中休息了0.5小时,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.解答下列问题:

(1)图中a的值为;
(2)当x>1.5(h)时,求甲车行驶路程y(km)与时间x(h)的函数关系式;
(3)当甲车行驶多长时间后,两车恰好相距40km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() .
.

(1)求证:![]() ;
;
(2)若![]() 的外角平分线以及
的外角平分线以及![]() 的平分线交于点
的平分线交于点![]() ,(1)结论是否成立?请在图中补全图形,写出结论,并说明理由.
,(1)结论是否成立?请在图中补全图形,写出结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF ∥BC交AB于E,交AC于F,过点G作GD⊥ AC于D,下列四个结论:①EF = BE+CF;②∠BGC= 90 °+![]() ∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=
∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=![]() mn.其中正确的结论有( )
mn.其中正确的结论有( )

A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】饮水机接通电源就进入自动程序,若在水温为![]() 时,接通电源后,水温
时,接通电源后,水温![]() 和时间
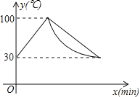
和时间![]() 的关系如图.开机加热时每分钟上升
的关系如图.开机加热时每分钟上升![]() ,加热到
,加热到![]() ,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至
,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至![]() ,饮水机自动开机,重复上述自动程序.若上午
,饮水机自动开机,重复上述自动程序.若上午![]() 开机,则
开机,则![]() 时能否喝到超过
时能否喝到超过![]() 的水?说明理由.
的水?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A.角平分线上的点到这个角两边的距离相等
B.角的内部到角的两边的距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com