
【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,以大于![]() EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )

A. 120° B. 30° C. 150° D. 60°
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在A、B 两地之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A,B两地同时开工,若干天后公路准确接通,若公路AB长8千米,另一条公路BC长是6千米,且BC的走向是北偏西42°,则A地到公路BC的距离是( )
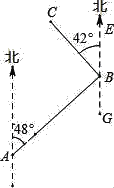
A. 6千米 B. 8千米 C. 10千米 D. 14千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于![]() MN长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( )
MN长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( )
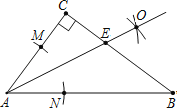
A.8B.7C.6D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
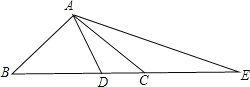
【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
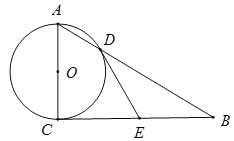
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系:_________;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC=_______时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)直接写出不等式k1x+b≥![]() 的解集;
的解集;
(3)M为线段PQ上一点,且MN⊥x轴于N,求△MON的面积最大值及对应的M点坐标.
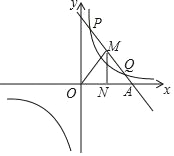
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.

(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;
∠C;
②AE+BF=EF;
③当∠C=90°时,E,F分别是AC,BC的中点;
④若OD=a,CE+CF=2b,则S△CEF=ab.
其中正确的是( )

A.①②B.③④C.①②④D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com