
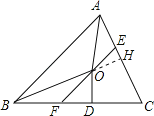
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;
∠C;
②AE+BF=EF;
③当∠C=90°时,E,F分别是AC,BC的中点;
④若OD=a,CE+CF=2b,则S△CEF=ab.
其中正确的是( )

A.①②B.③④C.①②④D.①③④
【答案】C
【解析】
根据角平分线的定义和三角形内角和定理判断①;根据角平分线的定义和平行线的性质判断②;根据三角形三边关系判断③;根据角平分线的性质判断④.
∵∠BAC和∠ABC的平分线相交于点O,
∴∠OBA=![]() ∠CBA,∠OAB=
∠CBA,∠OAB=![]() ∠CAB,
∠CAB,
∴∠AOB=180°﹣∠OBA﹣∠OAB
=180°﹣![]() ∠CBA﹣
∠CBA﹣![]() ∠CAB
∠CAB
=180°﹣![]() (180°﹣∠C)
(180°﹣∠C)
=90°+![]() ∠C,①正确;
∠C,①正确;
∵EF∥AB,
∴∠FOB=∠ABO,又∠ABO=∠FBO,
∴∠FOB=∠FBO,
∴FO=FB,
同理EO=EA,
∴AE+BF=EF,②正确;
当∠C=90°时,AE+BF=EF<CF+CE,
∴E,F不是AC,BC的中点,③错误;
作OH⊥AC于H,
∵∠BAC和∠ABC的平分线相交于点O,
∴点O在∠C的平分线上,
∴OD=OH,
∴S△CEF=![]() ×CF×OD
×CF×OD![]() ×CE×OH=ab,④正确.
×CE×OH=ab,④正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,以大于![]() EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )

A. 120° B. 30° C. 150° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
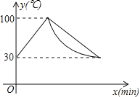
【题目】饮水机接通电源就进入自动程序,若在水温为![]() 时,接通电源后,水温
时,接通电源后,水温![]() 和时间
和时间![]() 的关系如图.开机加热时每分钟上升
的关系如图.开机加热时每分钟上升![]() ,加热到
,加热到![]() ,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至
,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至![]() ,饮水机自动开机,重复上述自动程序.若上午
,饮水机自动开机,重复上述自动程序.若上午![]() 开机,则
开机,则![]() 时能否喝到超过
时能否喝到超过![]() 的水?说明理由.
的水?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且|x1-x2|=2![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c过点A(0,2).
(1)若点(﹣![]() ,0)也在该抛物线上,求a,b满足的关系式;
,0)也在该抛物线上,求a,b满足的关系式;
(2)若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为心,OA为半径的圆与拋物线的另两个交点为B,C,且△ABC有一个内角为60°.
①求抛物线的解析式;
②若点P与点O关于点A对称,且O,M,N三点共线,求证:PA平分∠MPN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A.角平分线上的点到这个角两边的距离相等
B.角的内部到角的两边的距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC与△A'B'C在平面直角坐标系中的位置如图.

(1)分别写出B、B'的坐标:B______;B′______;
(2)若点P(a,b)是△ABC内部一点,则平移后△A'B'C内的对应点P′的坐标为______;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为菱形ABCD对角线的交点,M是射线CA上的一个动点(点M与点C、O、A都不重合),过点A、C分别向直线BM作垂线段,垂足分别为E、F,连接OE,OF.


(1)①依据题意补全图形;
②猜想OE与OF的数量关系为_________________.
(2)小东通过观察、实验发现点M在射线CA上运动时,(1)中的猜想始终成立.
小东把这个发现与同学们进行交流,通过讨论,形成了证明(1)中猜想的几种想法:
想法1:由已知条件和菱形对角线互相平分,可以构造与△OAE全等的三角形,从而得到相等的线段,再依据直角三角形斜边中线的性质,即可证明猜想;
想法2:由已知条件和菱形对角线互相垂直,能找到两组共斜边的直角三角形,例如其中的一组△OAB和△EAB,再依据直角三角形斜边中线的性质,菱形四边相等,可以构造一对以OE和OF为对应边的全等三角形,即可证明猜想.
……
请你参考上面的想法,帮助小东证明(1)中的猜想(一种方法即可).
(3)当∠ADC=120°时,请直接写出线段CF,AE,EF之间的数量关系是_________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com