
【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
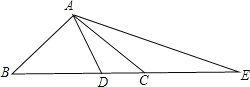
【答案】(1)450;(2)不改变;(3)∠DAE=![]() ∠BAC.
∠BAC.
【解析】
(1)要求∠DAE,必先求∠BAD和∠CAE,由∠BAC=90°,AB=AC,可求∠B=∠ACB=45°,又因为BD=BA,可求∠BAD=∠BDA=67.5°,再由CE=CA,可求∠CAE=∠E=22.5°,所以∠DAE=∠BAE-∠BAD=112.5°-67.5°=45°;
(2)先设∠CAE=x,由已知CA=CE可求∠ACB=∠CAE+∠E=2x,∠B=90°-2x,又因为BD=BA,所以∠BAD=∠BDA=x+45°,再根据三角形的内角和是180°,可求∠BAE=90°+x,即∠DAE=∠BAE-∠BAD=(90°+x)-(x+45°)=45度;
(3)可设∠CAE=x,∠BAD=y,则∠B=180°-2y,∠E=∠CAE=x,所以∠BAE=180°-∠B-∠E=2y-x,∠BAC=∠BAE-∠CAE=2y-x-x=2y-2x,即∠DAE=![]() ∠BAC.
∠BAC.
(1)∵AB=AC,∠BAC=![]() ,
,
∴∠B=∠ACB=![]() ,
,
∵BD=BA,
∴∠BAD=∠BDA=![]() (180∠B)=
(180∠B)=![]()
∵CE=CA,
∴∠CAE=∠E=![]() ∠ACB=
∠ACB=![]() ,
,
在△ABE中,∠BAE=180∠B∠E=![]() ,
,
∴∠DAE=∠BAE∠BAD=![]()
![]() =
=![]() ;
;
(2)不改变.
设∠CAE=x,
∵CA=CE,
∴∠E=∠CAE=x,
∴∠ACB=∠CAE+∠E=2x,
在△ABC中,∠BAC=![]() ,
,
∴∠B=![]() ∠ACB=
∠ACB=![]() 2x,
2x,
∵BD=BA,
∴∠BAD=∠BDA=![]() (180∠B)=x+
(180∠B)=x+![]() ,
,
在△ABE中,∠BAE=![]() ∠B∠E,=
∠B∠E,=![]() (
(![]() 2x)x=
2x)x=![]() +x,
+x,
∴∠DAE=∠BAE∠BAD,=(![]() +x)(x+
+x)(x+![]() )=
)=![]() ;
;
(3)∠DAE=![]() ∠BAC.
∠BAC.
理由:设∠CAE=x,∠BAD=y,
则∠B=![]() 2y,∠E=∠CAE=x,
2y,∠E=∠CAE=x,
∴∠BAE=![]() ∠B∠E=2yx,
∠B∠E=2yx,
∴∠DAE=∠BAE∠BAD=2yxy=yx,
∠BAC=∠BAE∠CAE=2yxx=2y2x,
∴∠DAE=![]() ∠BAC.
∠BAC.


科目:初中数学 来源: 题型:
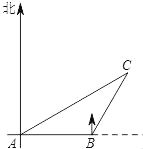
【题目】如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
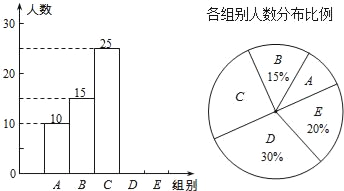
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 与等腰
与等腰![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 和
和![]() 相交于点
相交于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 与点
与点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④若
;④若![]() ,则
,则![]() .其中一定正确的结论的个数是( )
.其中一定正确的结论的个数是( )
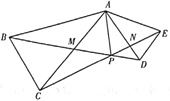
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海尔专卖店春节期间,销售10台Ⅰ型号洗衣机和20台Ⅱ型号洗衣机的利润为4000元,销售20台Ⅰ型号洗衣机和10台Ⅱ型号洗衣机的利润为3500元.
(1)求每台Ⅰ型号洗衣机和Ⅱ型号洗衣机的销售利润;
(2)该商店计划一次购进两种型号的洗衣机共100台,其中Ⅱ型号洗衣机的进货量不超过Ⅰ型号洗衣机的进货量的2倍,问当购进Ⅰ型号洗衣机多少台时,销售这100台洗衣机的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,以大于![]() EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )

A. 120° B. 30° C. 150° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地开往B地,甲车比乙车早出发2小时,并且在途中休息了0.5小时,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.解答下列问题:

(1)图中a的值为;
(2)当x>1.5(h)时,求甲车行驶路程y(km)与时间x(h)的函数关系式;
(3)当甲车行驶多长时间后,两车恰好相距40km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF ∥BC交AB于E,交AC于F,过点G作GD⊥ AC于D,下列四个结论:①EF = BE+CF;②∠BGC= 90 °+![]() ∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=
∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=![]() mn.其中正确的结论有( )
mn.其中正确的结论有( )

A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com