
【题目】如图,在△ ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF ∥BC交AB于E,交AC于F,过点G作GD⊥ AC于D,下列四个结论:①EF = BE+CF;②∠BGC= 90 °+![]() ∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=
∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=![]() mn.其中正确的结论有( )
mn.其中正确的结论有( )

A.1 个B.2 个C.3 个D.4 个
【答案】D
【解析】
根据BG,CG分别是∠ABC和∠ACB的平分线,EF ∥BC,可得EB=EG,FG=FC,从而证得①正确;根据三角形内角和定理即可求出②正确;根据角平分线的性质可知点G是△ABC的内心,从而可得③正确;连接AG,结合点G是内心,即可表示出△AEG和△AFG的面积,从而可知④正确.
∵BG,CG分别是∠ABC和∠ACB的平分线,
∴∠EBG=∠GBC,∠FCG=∠GCB
∵EF ∥BC
∴∠EGB=∠GBC,∠FGC=∠GCB
∴∠EBG=∠EGB,∠FCG=∠FGC
∴EB=EG,FG=FC
∴EF = BE+CF
故①正确;
在△ABC中,∠A=180°-(∠ABC+∠ACB)
在△GBC中,![]() ,
,
即![]()
所以②正确;
∵点G是∠ABC和∠ACB的平分线的交点,
∴点G是△ABC的内心
∴点G到△ABC各边的距离相等
故③正确;
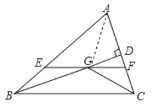
连接AG,
∵点G到△ABC各边的距离相等,GD=m,AE+AF=n,
∴![]()
故④正确;
综上答案选D.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AE=CD,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
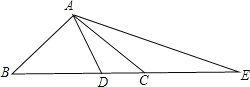
【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
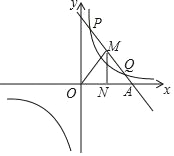
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)直接写出不等式k1x+b≥![]() 的解集;
的解集;
(3)M为线段PQ上一点,且MN⊥x轴于N,求△MON的面积最大值及对应的M点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.

(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
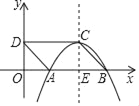
【题目】如图,ABCD位于直角坐标系中,AB=2,点D(0,1),以点C为顶点的抛物线y=ax2+bx+c经过x轴正半轴上的点A,B,CE⊥x轴于点E.
(1)求点A,B,C的坐标.
(2)将该抛物线向上平移m个单位恰好经过点D,且这时新抛物线交x轴于点M,N.
①求MN的长.
②点P是新抛物线对称轴上一动点,将线段AP绕点A顺时针旋转60°得AQ,则OQ的最小值为 (直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元.为了扩大销售,增加盈利,商场决定采取适当的降价措施.经调查发现,在一定范围内,衬衫的单价每下降
元.为了扩大销售,增加盈利,商场决定采取适当的降价措施.经调查发现,在一定范围内,衬衫的单价每下降![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件.
件.
![]() 如果商场通过销售这批衬衫每天获利
如果商场通过销售这批衬衫每天获利![]() 元,那么衬衫的单价应下降多少元?
元,那么衬衫的单价应下降多少元?
![]() 当每件衬衫的单价下降多少元时,每天通过销售衬衫获得的利润最大?最大利润为多少元?
当每件衬衫的单价下降多少元时,每天通过销售衬衫获得的利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,长方形ABCD中,AB=4,BC=![]() ,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )

A.4个B.5个C.6个D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com