
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

【答案】(1)BE=![]() AF;(2)无变化;证明见解析;(3)当正方形CDEF旋转到B,E,F三点共线时候,线段AF的长为
AF;(2)无变化;证明见解析;(3)当正方形CDEF旋转到B,E,F三点共线时候,线段AF的长为![]() ﹣1或
﹣1或![]() +1.
+1.
【解析】试题分析:(1)先利用等腰直角三角形的性质得出AD=![]() ,再得出BE=AB=2,即可得出结论;
,再得出BE=AB=2,即可得出结论;
(2)先利用三角函数得出![]() ,同理得出
,同理得出![]() ,夹角相等即可得出△ACF∽△BCE,进而得出结论;
,夹角相等即可得出△ACF∽△BCE,进而得出结论;
(3)分两种情况计算,当点E在线段BF上时,如图2,先利用勾股定理求出EF=CF=AD=![]() ,BF=
,BF=![]() ,即可得出BE=
,即可得出BE=![]() ﹣
﹣![]() ,借助(2)得出的结论,当点E在线段BF的延长线上,同前一种情况一样即可得出结论.
,借助(2)得出的结论,当点E在线段BF的延长线上,同前一种情况一样即可得出结论.
试题解析:(1)在Rt△ABC中,AB=AC=2,
根据勾股定理得,BC=![]() AB=2
AB=2![]() ,
,
点D为BC的中点,∴AD=![]() BC=
BC=![]() ,
,
∵四边形CDEF是正方形,∴AF=EF=AD=![]() ,
,
∵BE=AB=2,∴BE=![]() AF,
AF,
故答案为BE=![]() AF;
AF;
(2)无变化;
如图2,在Rt△ABC中,AB=AC=2,
∴∠ABC=∠ACB=45°,∴sin∠ABC=![]() ,
,
在正方形CDEF中,∠FEC=![]() ∠FED=45°,
∠FED=45°,
在Rt△CEF中,sin∠FEC=![]() ,
,
∴![]() ,
,
∵∠FCE=∠ACB=45°,∴∠FCE﹣∠ACE=∠ACB﹣∠ACE,∴∠FCA=∠ECB,
∴△ACF∽△BCE,∴![]() =
=![]() ,∴BE=
,∴BE=![]() AF,
AF,
∴线段BE与AF的数量关系无变化;
(3)当点E在线段AF上时,如图2,
由(1)知,CF=EF=CD=![]() ,
,
在Rt△BCF中,CF=![]() ,BC=2
,BC=2![]() ,
,
根据勾股定理得,BF=![]() ,∴BE=BF﹣EF=
,∴BE=BF﹣EF=![]() ﹣
﹣![]() ,
,
由(2)知,BE=![]() AF,∴AF=
AF,∴AF=![]() ﹣1,
﹣1,
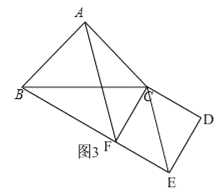
当点E在线段BF的延长线上时,如图3,
在Rt△ABC中,AB=AC=2,∴∠ABC=∠ACB=45°,∴sin∠ABC=![]() ,
,
在正方形CDEF中,∠FEC=![]() ∠FED=45°,
∠FED=45°,
在Rt△CEF中,sin∠FEC=![]() ,∴
,∴![]() ,
,
∵∠FCE=∠ACB=45°,∴∠FCB+∠ACB=∠FCB+∠FCE,∴∠FCA=∠ECB,
∴△ACF∽△BCE,∴![]() =
=![]() ,∴BE=
,∴BE=![]() AF,
AF,
由(1)知,CF=EF=CD=![]() ,
,
在Rt△BCF中,CF=![]() ,BC=2
,BC=2![]() ,
,
根据勾股定理得,BF=![]() ,∴BE=BF+EF=
,∴BE=BF+EF=![]() +
+![]() ,
,
由(2)知,BE=![]() AF,∴AF=
AF,∴AF=![]() +1.
+1.
即:当正方形CDEF旋转到B,E,F三点共线时候,线段AF的长为![]() ﹣1或
﹣1或![]() +1.
+1.


科目:初中数学 来源: 题型:
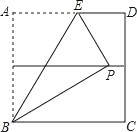
【题目】如图,正方形ABCD的面积为4,点F,G分别是AB,DC的中点,将点A折到FG上的点P处,折痕为BE,点E在AD上,则AE长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海尔专卖店春节期间,销售10台Ⅰ型号洗衣机和20台Ⅱ型号洗衣机的利润为4000元,销售20台Ⅰ型号洗衣机和10台Ⅱ型号洗衣机的利润为3500元.
(1)求每台Ⅰ型号洗衣机和Ⅱ型号洗衣机的销售利润;
(2)该商店计划一次购进两种型号的洗衣机共100台,其中Ⅱ型号洗衣机的进货量不超过Ⅰ型号洗衣机的进货量的2倍,问当购进Ⅰ型号洗衣机多少台时,销售这100台洗衣机的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地开往B地,甲车比乙车早出发2小时,并且在途中休息了0.5小时,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.解答下列问题:

(1)图中a的值为;
(2)当x>1.5(h)时,求甲车行驶路程y(km)与时间x(h)的函数关系式;
(3)当甲车行驶多长时间后,两车恰好相距40km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“金山”超市现有甲、乙两种糖果若干kg,两种糖果的售价和进价如表
糖果 | 甲种 | 乙种 |
售价 | 36元/kg | 20元/kg |
进价 | 30元/kg | 16元/kg |
(1)超市准备用甲、乙两种糖果混合成杂拌糖出售,混合后糖果的售价是27.2元/kg,现要配制这种杂拌糖果100/kg,需要甲、乙两种糖果各多少千克?
(2)“六一”儿童节前夕,超市准备用5000元购进甲、乙两种糖果共200kg,如何进货才能使这批糖果获得最大利润,最大利润是多少?(注:进货量只能为整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF ∥BC交AB于E,交AC于F,过点G作GD⊥ AC于D,下列四个结论:①EF = BE+CF;②∠BGC= 90 °+![]() ∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=
∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=![]() mn.其中正确的结论有( )
mn.其中正确的结论有( )

A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
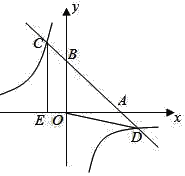
【题目】如图,直角坐标系xOy中,直线y=﹣x+b分别交x,y轴的正半轴于点A,B,交反比例函数y=﹣![]() 的图象于点C,D(点C在第二象限内),过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若
的图象于点C,D(点C在第二象限内),过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若![]() ,则CD的长为____.
,则CD的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列六个命题:①相等的角是对顶角;②两直线平行,同位角相等;③若一个三角形的两个内角分别为![]() 和
和![]() ,则这个三角形是直角三角形;④全等三角形的对应角相等。其中逆命题是假命题的个数有( )
,则这个三角形是直角三角形;④全等三角形的对应角相等。其中逆命题是假命题的个数有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂线平分线交AB于点F,交BC的延长线于点E,连接AE,DF.
求证:(1)∠EAD=∠EDA;(2)DF//AC;(3)∠EAC=∠B.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com