
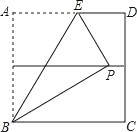
【题目】如图,正方形ABCD的面积为4,点F,G分别是AB,DC的中点,将点A折到FG上的点P处,折痕为BE,点E在AD上,则AE长为______.
【答案】![]()
【解析】
利用正方形ABCD的面积为4得到正方形ABCD的边长为2,再根据折叠的性质得BA=BP=2,∠ABE=∠PBE;由于点F,G分别是AB,DC的中点,则FG⊥AB,BF=1,在Rt△BPF中,由于PB=4,BF=2,根据含30度的直角三角形三边的关系得到得到∠FPB=30°,利用互余得∠ABP=60°,则∠ABE=30°,然后在Rt△ABE中根据含30度的直角三角形三边的关系求AE的长.
如图,
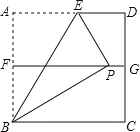
∵正方形ABCD的面积为4,
∴正方形ABCD的边长为2,
∵点A折到FG上的点P处,折痕为BE,
∴BA=BP=2,∠ABE=∠PBE,
∵点F,G分别是AB,DC的中点,
∴FG⊥AB,BF=1,
在Rt△BPF中,PB=4,BF=2,
∴∠FPB=30°,
∴∠ABP=60°,
∴∠ABE=30°,
在Rt△ABE中,AE=![]() AB=
AB=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12 米,BC=24 米,动点P从点A始沿边AB向B以2 米/秒的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4 米/秒的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为x 秒,四边形APQC的面积为y 米2.
(1)求y与x之间的函数关系式并写出自变量x的取值范围;
(2)四边形APQC的面积能否等于172米2.若能,求出运动的时间;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;(2)如图3,如果α=45°,AB=2,AE=4![]() ,求点G到BE的距离.
,求点G到BE的距离.
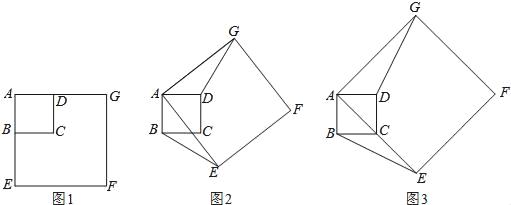
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家在甲、乙两家商场销售同一商品所获得的利润分别为![]() ,
,![]() (单位:元),
(单位:元),![]() ,
,![]() 与销售数量x(单位:件)的函数关系如图所示,试根据图象解决下列问题:
与销售数量x(单位:件)的函数关系如图所示,试根据图象解决下列问题:
(1)分别求出![]() ,
,![]() 关于x的函数关系式;
关于x的函数关系式;
(2)现厂家分配该商品800件给甲商场,400件给乙商场,当甲、乙商场售完这批商品后,厂家可获得的总利润是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AE=CD,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师给爱好学习的小军和小俊提出这样一个问题:如图①,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.

【变式探究】如图③,当点P在BC延长线上时,其余条件不变,求证:PD﹣PE=CF;请运用上述解答中所积累的经验和方法完成下题:
【结论运用】如图④,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,且A2O=2A1O,…,依此规律,得到等腰直角三角形A2018OB2018,则点A2018的坐标为_____.
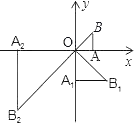
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com