
【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b],对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
(2)若一次函数y=kx+b(k>0)是闭区间[m,n]上的“闭函数”,求此函数的解析式.
【答案】(1)反比例函数y=![]() 是闭区间[1,2015]上的“闭函数”,理由见解析;(2)y=x.
是闭区间[1,2015]上的“闭函数”,理由见解析;(2)y=x.
【解析】
试题分析:(1)根据反比例函数y=![]() 的单调区间进行判断;
的单调区间进行判断;
(2)根据新定义运算法则列出关于系数k、b的方程组![]() ,通过解该方程组即可求得系数k、b的值.
,通过解该方程组即可求得系数k、b的值.
解:(1)反比例函数y=![]() 是闭区间[1,2015]上的“闭函数”.理由如下:
是闭区间[1,2015]上的“闭函数”.理由如下:
反比例函数y=![]() 在第一象限,y随x的增大而减小,
在第一象限,y随x的增大而减小,
当x=1时,y=2015;
当x=2015时,y=1,
所以,当1≤x≤2015时,有1≤y≤2015,符合闭函数的定义,故
;
(2)∵k>0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而增大,
∴![]() ,
,
解得![]() .
.
∴此函数的解析式是y=x.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.
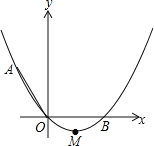
(1)求a,b的值;
(2)连结OM,求∠AOM的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年12月6日,我县举行了2018年商品订货交流会,参加会议的每两家公司之间都签订了一份合同,所有参会公司共签订了28份合同,共有多少家公司参加了这次会议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.

(1)求证:△ABN≌△CDM;
(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;
(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
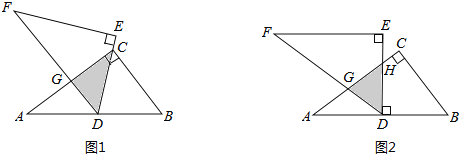
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是国外城市与北京的时差 (带正号的数表示同一时刻比北京时间早的时数)
城市 | 纽约 | 巴黎 | 东京 | 多伦多 |
时差(时) | ﹣13 | ﹣7 | +1 | ﹣12 |
如果现在东京时间是16:00,那么纽约时间是__.(以上均为24小时制)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com