
分析 根据题意可知点C在x轴上或者在y轴上,通过画图分析,符合要求的有四种情况,根据AC+BC=10,可以确定点C的坐标.
解答 解:如下图所示: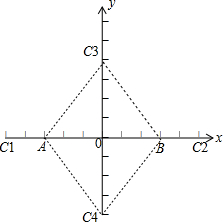
∵已知点A(-3,0),B(3,0),点C在坐标轴上,且AC+BC=10,
∴点C所在的位置有四种情况:
第一种情况:点C在点A的左侧.
设点C的坐标为(x,0).
∵AC+BC=10,点A(-3,0),B(3,0),
∴(-3-x)+(3-x)=10.
解得,x=-5.
∴点C的坐标为(-5,0),点A(-3,0),B(3,0),
第二种情况:点C在点B的右侧.
设点C的坐标为(x,0).
∵AC+BC=10,
∴[x-(-3)]+(x-3)=10.
解得,x=5.
∴点C的坐标为(5,0).
第三种情况:点C在y轴上方.
设点C的坐标为(0,y).
∵AC+BC=10,点A(-3,0),B(3,0),
∴AC=BC=5,32+y2=52.
解得,y=±4.
∵点C在y轴上方,
∴点C的坐标为(0,4).
第四种情况:点C在y轴下方.
设点C的坐标为(0,y).
∵AC+BC=10,点A(-3,0),B(3,0),
∴AC=BC=5,32+y2=52.
解得,y=±4.
∵点C在y轴下方,
∴点C的坐标为(0,-4).
故答案为:(-5,0),(5,0),(0,4),(0,-4).
点评 本体主要考查坐标与图形的关系,关键是可以根据题目中的信息把点C的几种可能性都考虑到,画出相应的图形.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
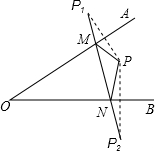 如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=20,则△PMN的周长为20.
如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=20,则△PMN的周长为20.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
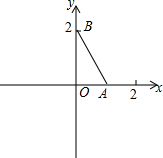 如图,在平面直角坐标系中,已知点A(1,0)和点B(0,2),点C在x轴上,若以A、B、C为顶点构成的三角形是等腰三角形,则满足条件的点C的坐标是(1-$\sqrt{5}$,0),(-1,0),(-$\frac{3}{2}$,0).
如图,在平面直角坐标系中,已知点A(1,0)和点B(0,2),点C在x轴上,若以A、B、C为顶点构成的三角形是等腰三角形,则满足条件的点C的坐标是(1-$\sqrt{5}$,0),(-1,0),(-$\frac{3}{2}$,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com