
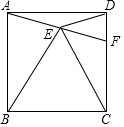
 如图,正方形ABCD中,以BC为边向正方形内部作等边△BCE,连接AE并延长交CD于F,连接DE,下列结论:①AE=DE;②∠CEF=45°;③AE=EF;④△DEF∽△ABE,其中正确的结论共有( )
如图,正方形ABCD中,以BC为边向正方形内部作等边△BCE,连接AE并延长交CD于F,连接DE,下列结论:①AE=DE;②∠CEF=45°;③AE=EF;④△DEF∽△ABE,其中正确的结论共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用正方形的性质、等边三角形的性质,想办法求出相关角的度数,即可一一解决问题.
解答 解:∵ 四边形ABCD是正方形,
四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠ADC=90°,
∵△EBC是等边三角形,
∴BC=BE=CE,∠EBC=∠EBC=∠ECB=60°,
∴∠ABE=∠ECF=30°,
∵BA=BE,EC=CD,
∴∠BAE=∠BEA=∠CED=∠CDE=$\frac{1}{2}$(180°-30°)=75°,
∴∠EAD=∠EDA=15°,
∴EA=ED,故①正确,
∴∠DEF=∠EAD+∠ADE=30°,
∴∠CEF=∠CED-∠DEF=45°,故②正确,
∵∠EDF=∠AFD=75°,
∴ED=EF,
∴AE=EF,故③正确,
∵∠BAE=∠BEA=∠EDF=∠EFD=75°,
∴△DEF∽△ABE,故④正确,
故选D.
点评 本题考查正方形的性质、等边三角形的性质、相似三角形的判定、等腰三角形的判定等知识,解题的关键是灵活应用正方形以及等边三角形的性质,通过计算角度解决问题,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$<-2<0.02<0 | B. | -$\frac{1}{2}$<-2<0<0.02 | C. | -2<-$\frac{1}{2}$<0.02<0 | D. | -2<-$\frac{1}{2}$<0<0.02 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 2x-2 | C. | -4 | D. | 2-2x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com