
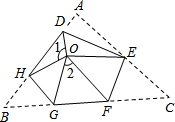
 如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为180°.
如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为180°. 分析 根据翻折变换前后对应角不变,故∠B=∠HOG,∠A=∠DOE,∠C=∠EOF,∠1+∠2+∠HOG+∠EOF+∠DOE=360°,进而求出∠1+∠2的度数.
解答 解:∵将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,
∴∠B=∠HOG,∠A=∠DOE,∠C=∠EOF,∠1+∠2+∠HOG+∠EOF+∠DOE=360°,
∵∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°,
∴∠1+∠2=360°-180°=180°,
故答案为:180.
点评 此题主要考查了翻折变换的性质和三角形的内角和定理,根据已知得出∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°是解题关键.


科目:初中数学 来源: 题型:解答题
 如图,我们把杜甫(绝句)整齐排列放在平面直角坐标系中:
如图,我们把杜甫(绝句)整齐排列放在平面直角坐标系中:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3•a2=a6 | B. | $\sqrt{9}$=±3 | C. | ($\frac{1}{2}$)-1=-2 | D. | (π-3.14)0=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
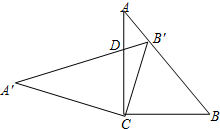 在Rt△ABC中,∠C=90°,cosB=$\frac{3}{5}$,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么$\frac{B′D}{CD}$等于( )
在Rt△ABC中,∠C=90°,cosB=$\frac{3}{5}$,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么$\frac{B′D}{CD}$等于( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{7}{20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
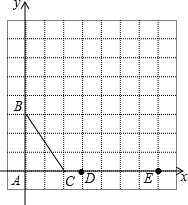 如图,在方格纸中,以每个小方格的边长为单位1,△ABC和△EPD的顶点均在格点上,请你提供一个符合条件的点P,使△ABC与以E、P、D为顶点的三角形相似,则点P所在的格点坐标可以是(3,6).
如图,在方格纸中,以每个小方格的边长为单位1,△ABC和△EPD的顶点均在格点上,请你提供一个符合条件的点P,使△ABC与以E、P、D为顶点的三角形相似,则点P所在的格点坐标可以是(3,6).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com