
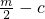 )是直线MC上的点
)是直线MC上的点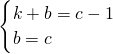 ,
,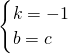
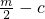 )是直线MC上的点,
)是直线MC上的点, -c=-m+c…①
-c=-m+c…① -c)在抛物线上,
-c)在抛物线上, -c=m2-2(-m)+c…②
-c=m2-2(-m)+c…②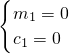 (舍),
(舍),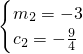
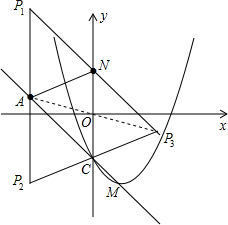 故抛物线对应的函数式:y=x2-2x-
故抛物线对应的函数式:y=x2-2x- .
. )、C(0,-
)、C(0,- )、N(0,
)、N(0, );
); AP,已知:CN=
AP,已知:CN= ,则有:
,则有: 个单位,得 P1(-3,
个单位,得 P1(-3, );
); 个单位,得 P2(-3,-
个单位,得 P2(-3,- );
); );
); ),
), )时,以A、C、P、N为顶点的四边形是平行四边形.
)时,以A、C、P、N为顶点的四边形是平行四边形. -c)在直线MC上,且点B(-m,
-c)在直线MC上,且点B(-m, -c)在抛物线上,通过联立方程组即可求出m、c的值.
-c)在抛物线上,通过联立方程组即可求出m、c的值.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)求b+c的值;
(1)求b+c的值;查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com