
如图,在平面直角坐标系 中,一次函数
中,一次函数 (a为常数)的图象与y轴相交于点A,与函数
(a为常数)的图象与y轴相交于点A,与函数 的图象相交于点B
的图象相交于点B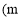 ,
, .
.
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.

(1)(2,1),y=x-1;(2)(0,1)或(0,3).
【解析】
试题分析:(1)由点在函数图象上,得到点的坐标满足函数解析式,利用待定系数法即可求得.
(2)分两种情况,一种是∠BPA=90°,另一种是∠PBA=90°,所以有两种答案.
试题解析:(1)∵B在的图象上,
∴把B(m,1)代入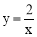 得m=2.
得m=2.
∴B点的坐标为(2,1).
∵B(2,1)在直线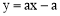 (a为常数)上,∴1=2a-a,∴a=1.
(a为常数)上,∴1=2a-a,∴a=1.
∴一次函数的解析式为y=x-1.
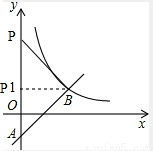
(2)如图,过B点向y轴作垂线交y轴于P点.此时∠BPA=90°.
∵B点的坐标为(2,1)∴P点的坐标为(0,1).
当PB⊥AB时,
在Rt△P1AB中,PB=2,PA=2,∴AB=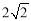 .
.
在等腰直角三角形PAB中,PB=PA=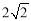 ,
,
∴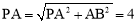 .∴OP=4-1=3.
.∴OP=4-1=3.
∴P点的坐标为(0,3).
∴P点的坐标为(0,1)或(0,3).
考点:1.反比例函数与一次函数的交点问题;2.分类思想的应用.


科目:初中数学 来源:2013-2014学年北京市燕山区中考一模数学试卷(解析版) 题型:解答题
阅读下面材料:
如果一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四边形”.如图1 所示,平行四边形ABCD即为△ABC的“友好平行四边形”.
请解决下列问题:
(1)仿照以上叙述,说明什么是一个三角形的“友好矩形”;
(2)若△ABC是钝角三角形,则△ABC显然只有一个“友好矩形”, 若△ABC是直角三角形,其“友好矩形”有 个;
(3)若△ABC是锐角三角形,且 ,如图2,请画出△ABC的所有“友好矩形”;指出其中周长最小的“友好矩形”并说明理由.
,如图2,请画出△ABC的所有“友好矩形”;指出其中周长最小的“友好矩形”并说明理由.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市燕山区中考一模数学试卷(解析版) 题型:选择题
如图所示,AB∥CD,点E在CB的延长线上.若∠ABE=70°,则∠ECD的度数为( )

A.20° B.70° C .100° D.110°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区中考一模数学试卷(解析版) 题型:解答题
在平面直角坐标系 中,二次函数
中,二次函数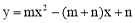 (
(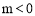 )的图象与
)的图象与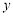 轴正半轴交于A点.
轴正半轴交于A点.
(1)求证:该二次函数的图象与x轴必有两个交点;
(2)设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;
(3)在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当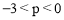 时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区中考一模数学试卷(解析版) 题型:选择题
下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 与方差
与方差 :
:
| 甲 | 乙 | 丙 | 丁 |
平均数 | 561 | 560 | 561 | 560 |
方差 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com