
如图1,在平面直角坐标系中,O为坐标原点,P是反比例函数y=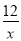 (x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
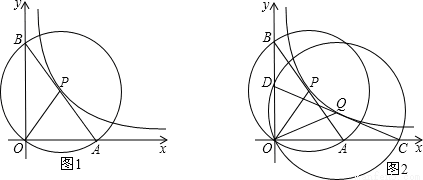
(1)求证:线段AB为⊙P的直径;
(2)求△AOB的面积;
(3)如图2,Q是反比例函数y=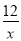 (x>0)图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D.求证:DO•OC=BO•OA.
(x>0)图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D.求证:DO•OC=BO•OA.
(1)证明见解析;(2)24;(3)证明见解析.
【解析】
试题分析:(1)∠AOB=90°,由圆周角定理的推论,可以证明AB是⊙P的直径;
(2)将△AOB的面积用含点P坐标的表达式表示出来,容易计算出结果;
(3)对于反比例函数上另外一点Q,⊙Q与坐标轴所形成的△COD的面积,依然不变,与△AOB的面积相等.
试题解析:(1)证明:∵∠AOB=90°,且∠AOB是⊙P中弦AB所对的圆周角,
∴AB是⊙P的直径.
(2)【解析】
设点P坐标为(m,n)(m>0,n>0),
∵点P是反比例函数y=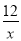 (x>0)图象上一点,
(x>0)图象上一点,
∴mn=12.
如图,过点P作PM⊥x轴于点M,PN⊥y轴于点N,则OM=m,ON=n.
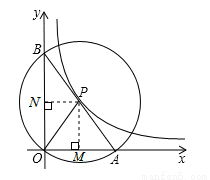
由垂径定理可知,点M为OA中点,点N为OB中点,
∴OA=2OM=2m,OB=2ON=2n,
∴S△AOB=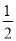 BO•OA=
BO•OA=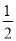 ×2n×2m=2mn=2×12=24.
×2n×2m=2mn=2×12=24.
(3)证明:∵以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D,∠COD=90°,
∴DC是⊙Q的直径.
若点Q为反比例函数y=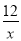 (x>0)图象上异于点P的另一点,
(x>0)图象上异于点P的另一点,
参照(2),同理可得:S△COD=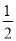 DO•CO=24,
DO•CO=24,
则有:S△COD=S△AOB=24,即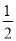 BO•OA=
BO•OA=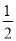 DO•CO,
DO•CO,
∴DO•OC=BO•OA.
考点:反比例函数综合题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源:2014-2015学年江苏省扬州市邗江区八年级上学期期中测试数学试卷(解析版) 题型:填空题
如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是___________________ 。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宝应县九年级上学期期中考试数学试卷(解析版) 题型:解答题
已知关于x的一元二次方程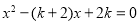 .
.
(1)试说明无论 取何值时,这个方程一定有实数根;
取何值时,这个方程一定有实数根;
(2)若等腰△ABC的一边长 ,另两边长
,另两边长 、
、 恰好是这个方程的两个根 ,求△ABC的周长.
恰好是这个方程的两个根 ,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宝应县九年级上学期期中考试数学试卷(解析版) 题型:选择题
如果关于x的一元二次方程 有两个不相等的实数根,那么
有两个不相等的实数根,那么 的取值范围是
的取值范围是
A. >
> B.
B. >
> 且
且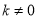
C. <
< D.
D. ≥
≥ 且
且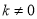
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期期中考试数学试卷(解析版) 题型:解答题
已知四边形ABCD顶点都在4×4的正方形网格格点上,如图所示,

(1)请画出四边形ABCD的外接圆,并标明圆心M的位置;
(2)这个圆中弦BC所对的圆周角的度数是 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省七年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分8分)若2a2-4ab+b2与一个多项式的差是-3a2+2ab-5b2,试求这个多项式。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省七年级上学期期中考试数学试卷(解析版) 题型:选择题
对于有理数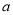 、
、 ,定义
,定义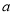 ⊙
⊙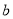
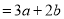 ,则[(x+y) ⊙(x-y)] ⊙3x化简后得( )
,则[(x+y) ⊙(x-y)] ⊙3x化简后得( )
A.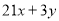 B.
B.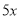 C.0 D.
C.0 D.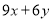
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com