
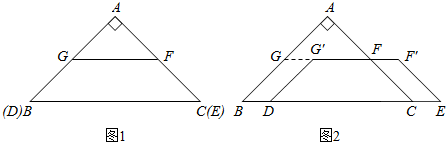
���� ��1���������ε���λ�߶�����֪��FG��BC����$GF=\frac{1}{2}BC$���Ӷ��õ���AGF�ס�ABC�������Ʊ�Ϊ1��2�������������ε�����ȵ������Ʊȵ�ƽ����֪����AGF���ABC���������1��4��
��2��������������������Ǻ���ֵ�����AC�ij�Ϊ4���Ӷ��õ�FC=2����ΪFC��EF'��CE��FF'���ı���CEF'F��ƽ���ı��Σ���CE=CF=2ʱ���ı���CEF'FΪ���Σ��Ӷ��ɵõ�x=2��
�ڵ�0��x��2$\sqrt{2}$ʱ����ͼ3��ʾ������F��FM��BC������ΪM�������FG=2$\sqrt{2}$��FM=$\sqrt{2}$�������ε������ʽ��֪S����G��DCF=$\frac{1}{2}��G��F+DC��•FM$=6-$\sqrt{2}x$���ʴ�y��x�ĺ�����ϵʽΪy=6-$\sqrt{2}x$����2$\sqrt{2}$��x��4$\sqrt{2}$ʱ����ͼ4��ʾ������P��PM��BC������ΪM����D��C=DC-DD��=4$\sqrt{2}$-x��Ȼ����֤��PM=$\frac{1}{2}D��C$=$\frac{1}{2}����4\sqrt{2}-x��$������������ε������ʽ��֪����PD��C�����=$\frac{1}{2}D��C•PM$=$\frac{1}{4}{x}^{2}-2\sqrt{2}x+8$���ʴ˿ɵó�y��x�ĺ�����ϵʽ��
��� �⣺��1����ͼ1��ʾ��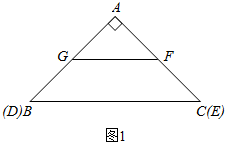
��G��F�ֱ���AB��AC���е㣬
��FG��BC����$GF=\frac{1}{2}BC$��
���AGF�ס�ABC����$\frac{GF}{BC}=\frac{1}{2}$��
�����������ε�����ȵ������Ʊȵ�ƽ����֪����AGF���ABC���������1��4��
��2����������
���ɣ���ͼ2��ʾ��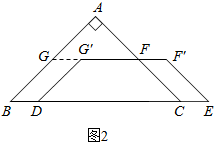
�ߡ�A=90�㣬AB=AC��
���ACB=45�㣮
��cos45��=$\frac{\sqrt{2}}{2}$��
��$\frac{AC}{BC}=\frac{\sqrt{2}}{2}$����$\frac{AC}{4\sqrt{2}}=\frac{\sqrt{2}}{2}$��
��AC=4��
��CF=2��
��FC��EF'��CE��FF'��
���ı���CEF'F��ƽ���ı��Σ�
�൱$CE=CF=\frac{1}{2}AC=2$ʱ���ı���CEF'FΪ���Σ�
��x=2��
�൱x=2��ʱ���ı���CEF'FΪ���Σ�
�ڵ�0��x��2$\sqrt{2}$ʱ����ͼ3��ʾ������F��FM��BC������ΪM��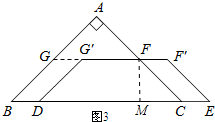
��$GF=\frac{1}{2}BC$
��FG=2$\sqrt{2}$��
��FC=2����FMC=90�㣬��FCB=45�㣬
��sin45��=$\frac{FM}{EC}=\frac{\sqrt{2}}{2}$����$\frac{FM}{2}=\frac{\sqrt{2}}{2}$��
��FM=$\sqrt{2}$��
S����G��DCF=$\frac{1}{2}��G��F+DC��•FM$=$\frac{1}{2}��2\sqrt{2}-x+4\sqrt{2}-x����\sqrt{2}$=6-$\sqrt{2}x$��
��y��x�ĺ�����ϵʽΪy=6-$\sqrt{2}x$��
��2$\sqrt{2}$��x��4$\sqrt{2}$ʱ����ͼ4��ʾ������P��PM��BC������ΪM��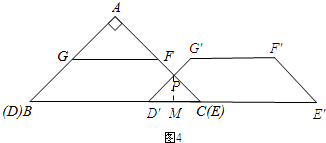
D��C=DC-DD��=4$\sqrt{2}$-x��
�ߡ�PDCΪ����ֱ�������Σ�PM��D��C��
��PM=$\frac{1}{2}D��C$=$\frac{1}{2}����4\sqrt{2}-x��$��
���PD��C�����=$\frac{1}{2}D��C•PM$=$\frac{1}{2}����4\sqrt{2}-x����\frac{1}{2}����4\sqrt{2}-x��$=$\frac{1}{4}{x}^{2}-2\sqrt{2}x+8$��
��y��x�ĺ�����ϵʽΪy=$\frac{1}{4}{x}^{2}-2\sqrt{2}x+8$��
����������y��x�ĺ�����ϵΪy=6$\left\{\begin{array}{l}{6-\sqrt{2}x��0��x��2\sqrt{2}��}\\{\frac{1}{4}{x}^{2}-2\sqrt{2}x+8��2\sqrt{2}��x��4\sqrt{2}��}\end{array}\right.$��
���� ������Ҫ������������ε���λ�߶���������ֱ�������ε����ʺ��ж������������ε����ʡ�ƽ�Ƶ������Լ������κ����ε������ʽ���ۺ�Ӧ�ã����ú�x�Ĵ���ʽ����ʾ�����κ������εĵߵij����ǽ���Ĺؼ���


 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+$\frac{1}{3}$��y+$\frac{1}{3}$ | B�� | x-3��y-3 | C�� | $\frac{x}{3}$��$\frac{y}{3}$ | D�� | -3x��-3y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��У��ʦ�ȼ�У��ʦ�˾����20Ԫ���Ҽ�У��ʦ����������У��ʦ��������20% | |
| B�� | ��У��ʦ����У��ʦ�˾����20Ԫ������У��ʦ�������ȼ�У��ʦ��������20% | |
| C�� | ��У��ʦ����У��ʦ�˾����20Ԫ���Ҽ�У��ʦ����������У��ʦ��������20% | |
| D�� | ��У��ʦ�ȼ�У��ʦ�˾����20Ԫ������У��ʦ�������ȼ�У��ʦ��������20% |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
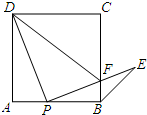 ��ͼ����P��������ABCD��AB��һ�㣨�����A��B�غϣ�������PD�����߶�PD�Ƶ�P˳ʱ�뷽����ת90��õ��߶�PE��PE����BC�ڵ�F������BE��DF��
��ͼ����P��������ABCD��AB��һ�㣨�����A��B�غϣ�������PD�����߶�PD�Ƶ�P˳ʱ�뷽����ת90��õ��߶�PE��PE����BC�ڵ�F������BE��DF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��֪a��b��c�������ε����߳�����a2+b2=c2 | |
| B�� | ��ֱ���������У����߳��͵�ƽ�����ڵ����߳���ƽ�� | |
| C�� | ��Rt��ABC�У�����C=90�㣬�������ζ�Ӧ����������a2+b2=c2 | |
| D�� | ��Rt��ABC�У�����A=90�㣬�������ζ�Ӧ����������a2+b2=c2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
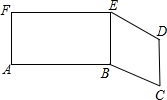 ��ͼ����һ��ֽƬ��������EB����ֽƬ����Ϊ����FABE������EBCD�����㻭һ��ֱ�߰�����ֽƬ�ֳ������ȵ������֣���˵�����ɣ�
��ͼ����һ��ֽƬ��������EB����ֽƬ����Ϊ����FABE������EBCD�����㻭һ��ֱ�߰�����ֽƬ�ֳ������ȵ������֣���˵�����ɣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com