
分析 分类讨论点C在AB上,点C在AB的延长线上,根据线段的中点的性质,可得BM、BN的长,根据线段的和差,可得答案.
解答 解:(1)①点C在线段AB上,如图:
∵点M是线段AB的中点,点N是线段BC的中点,
∴MB=$\frac{1}{2}$AB=3,BN=$\frac{1}{2}$CB=2,
∴MN=BM-BN=3-2=1cm;
②点C在线段AB的延长线上,如图:

∵点M是线段AB的中点,点N是线段BC的中点,
∴MB=$\frac{1}{2}$AB=3,BN=$\frac{1}{2}$CB=2,
∴MN=MB+BN=3+2=5cm.
(2)①点C在线段AB上,如图:
∵点M是线段AB的中点,点N是线段BC的中点,
∴MB=$\frac{1}{2}$AB=$\frac{1}{2}$a,BN=$\frac{1}{2}$CB=$\frac{1}{2}$b,
∴MN=BM-BN=$\frac{a-b}{2}$cm;
(2)点C在线段AB的延长线上,如图:

∵点M是线段AB的中点,点N是线段BC的中点,
∴MB=$\frac{1}{2}$AB=$\frac{1}{2}$a,BN=$\frac{1}{2}$CB=$\frac{1}{2}$b,
∴MN=MB+BN=$\frac{a+b}{2}$cm.
故答案为:$\frac{a-b}{2}$或$\frac{a+b}{2}$.
点评 本题考查了两点间的距离,分类讨论是解题关键,根据线段中点的性质,线段的和差,可得出答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 十分位 | B. | 百分位 | C. | 千位 | D. | 百位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
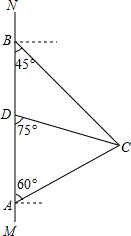 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距$50(\sqrt{3}+1)$海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距$50(\sqrt{3}+1)$海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com