
 如图,△ABC中,AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )
如图,△ABC中,AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}-1}{4}$ | C. | $\frac{\sqrt{5}+1}{4}$ | D. | $\frac{\sqrt{5}+1}{2}$ |
分析 先根据等腰三角形的性质与判定以及三角形内角和定理得出∠EBC=36°,∠BEC=72°,AE=BE=BC.再证明△BCE∽△ABC,根据相似三角形的性质列出比例式$\frac{CE}{BC}$=$\frac{BE}{AC}$,求出AE,然后在△ADE中利用余弦函数定义求出cosA的值.
解答 解:∵△ABC中,AB=AC=4,∠C=72°,
∴∠ABC=∠C=72°,∠A=36°,
∵D是AB中点,DE⊥AB,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠EBC=∠ABC-∠ABE=36°,
∠BEC=180°-∠EBC-∠C=72°,
∴∠BEC=∠C=72°,
∴BE=BC,
∴AE=BE=BC.
设AE=x,则BE=BC=x,EC=4-x.
在△BCE与△ABC中,
$\left\{\begin{array}{l}{∠CBE=∠BAC=36°}\\{∠C=∠ABC=72°}\end{array}\right.$,
∴△BCE∽△ABC,
∴$\frac{CE}{BC}$=$\frac{BE}{AC}$,即$\frac{4-x}{x}=\frac{x}{4}$,
解得x=-2±2$\sqrt{5}$(负值舍去),
∴AE=-2+2$\sqrt{5}$.
在△ADE中,∵∠ADE=90°,
∴cosA=$\frac{AD}{AE}$=$\frac{2}{-2+2\sqrt{5}}=\frac{\sqrt{5}+1}{4}$=.
故选C.
点评 本题考查了解直角三角形,等腰三角形的性质与判定,三角形内角和定理,线段垂直平分线的性质,相似三角形的判定与性质,难度适中.证明△BCE∽△ABC是解题的关键.


科目:初中数学 来源: 题型:选择题
| 时刻 | 9:00 | 9:45 | 12:00 |
| 碑上的数 | 是一个两位数,数字之和是9 | 十位与个位数字与9:00时所看到的正好相反 | 比9:00时看到的两位数中间多了个0 |
| A. | 54 | B. | 45 | C. | 36 | D. | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
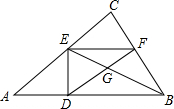 如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,AB上有一动点D以每秒4个单位的速度从点A向点B运动,当点D运动到点B时停止运动.过点D作DE⊥AB,垂足为点D,过点E作EF∥AB交BC于点F,连接BE交DF于点G,设点D运动的时间为t,当S△BDG=4S△EFG时,t的值为( )
如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,AB上有一动点D以每秒4个单位的速度从点A向点B运动,当点D运动到点B时停止运动.过点D作DE⊥AB,垂足为点D,过点E作EF∥AB交BC于点F,连接BE交DF于点G,设点D运动的时间为t,当S△BDG=4S△EFG时,t的值为( )| A. | t=$\frac{14}{17}$ | B. | t=$\frac{12}{10}$ | C. | t=$\frac{10}{17}$ | D. | t=$\frac{8}{17}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将三角尺ABC的一边AC沿位置固定的直尺推移得到△DEF,下列结论不一定正确的是( )
如图,将三角尺ABC的一边AC沿位置固定的直尺推移得到△DEF,下列结论不一定正确的是( )| A. | DE∥AB | B. | 四边形ABED是平行四边形 | ||
| C. | AD∥BE | D. | AD=AB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,?ABCD中,BC=2AB,E为AD中点,过点C作CF⊥AB于点F,垂足F落在线段AB上,连结FE并延长与CD的延长线交于点G,则下列结论:①CE平分∠BCG;②CE=EF;③∠DEF=3∠AFE;④当AF=BF时,S△BCF=S△CEF,正确的有( )
如图,?ABCD中,BC=2AB,E为AD中点,过点C作CF⊥AB于点F,垂足F落在线段AB上,连结FE并延长与CD的延长线交于点G,则下列结论:①CE平分∠BCG;②CE=EF;③∠DEF=3∠AFE;④当AF=BF时,S△BCF=S△CEF,正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com