
【题目】如图,直线 CB 和射线 OA,CB//OA,点 B 在点 C 的右侧.且满足∠OCB=∠OAB=100°,连接线段 OB,点 E、F 在直线 CB 上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠BOE
(2)当点 E、F 在线段 CB 上时(如图 1),∠OEC 与∠OBA 的和是否是定值?若是,求出这个值;若不是,说明理由。
(3)如果平行移动 AB,点 E、F 在直线 CB 上的位置也随之发生变化.当点 E、F 在点 C 左侧时,∠OEC 和∠OBA 之间的数量关系是否发生变化?若不变,说明理由;若变化,求出他们之间的关系式.

科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一点,PA=PC,∠C=30°.
(1)求证:CP是⊙O的切线.
(2)若⊙O的直径为8,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E在对角线BD上,且∠DAE=67.5°,EF⊥AB,垂足为F,则EF的长为( )

A. 1B. ![]() C. 4-2
C. 4-2![]() D. 3
D. 3![]() -4
-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济快速发展,环境问题越来越受到人们的关注校为了了解节能减排、垃圾分类等知 识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类, 并将结果绘制成以下两幅不完整的统计图,请根据统计图回答下列问题:

(1)本次调查的学生共有 人;
(2)将条形统计图补充完整;
(3)“非常了解”的![]() 人中有
人中有![]() ,两名男生,
,两名男生,![]() ,两名女生,若从中随机抽取两人去参加环保 知识竞赛,请用画树状图或列表的方法,求恰好抽到
,两名女生,若从中随机抽取两人去参加环保 知识竞赛,请用画树状图或列表的方法,求恰好抽到![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某品牌的饮料有大瓶装与小瓶装之分.某超市花了3800元购进一批该品牌的饮料共1000瓶,其中大瓶和小瓶饮料的进价及售价如下表所示:
大瓶 | 小瓶 | |
进价(元/瓶) | 5 | 2 |
售价(元/瓶) | 7 | 3 |
(1)该超市购进大瓶和小瓶饮料各多少瓶?
(2)在大瓶饮料售出200瓶,小瓶饮料售出100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点A,C,D在⊙O上,过D作PF∥AC交⊙O于F,交AB于E,且∠BPF=∠ADC.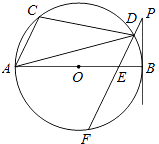
(1)判断直线BP和⊙O的位置关系,并说明你的理由;
(2)当⊙O的半径为 ![]() ,AC=2,BE=1时,求BP的长.
,AC=2,BE=1时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,动点A,B同时从原点O出发,运动的速度都是每秒1个单位,动点A沿x轴正方向运动,动点B沿y轴正方向运动,以OA,OB为邻边建立正方形OACB,抛物线y=﹣x2+bx+c经过B,C两点,假设A,B两点运动的时间为t秒: 根据
根据
(1)直接写出直线OC的解析式;
(2)当t=3秒时,求此时抛物线的解析式;此时抛物线上是否存在一点D,使得S△BCD=6?若存在,求出点D的坐标;若不存在,说明理由;
(3)在(2)的条件下,有一条平行于y轴的动直线l,交抛物线于点E,交直线OC于点F,若以O、B、E、F四个点构成的四边形是平行四边形,求点F的坐标;
(4)在动点A、B运动的过程中,若正方形OACB内部有一个点P,且满足OP= ![]() ,CP=2,∠OPA=135°,直接写出此时AP的长度.
,CP=2,∠OPA=135°,直接写出此时AP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张,不放回,再从剩下的卡片中随机抽取一张.
(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果,(卡片用A,B,C,D表示);
(2)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,0),B(0,4),C(3,t+4),D(3,t). 记N(t)为![]() ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为
ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为
A. 6、7B. 7、8C. 6、7、8D. 6、8、9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com