
����Ŀ����ͼ1����ABC�͡�CDE���ǵ���ֱ�������Σ���C=90�㣬����CDE�Ƶ�C��ʱ����תһ���ǶȦ���0�㣼����90�㣩��ʹ��A��D��E��ͬһֱ���ϣ�����AD��BE��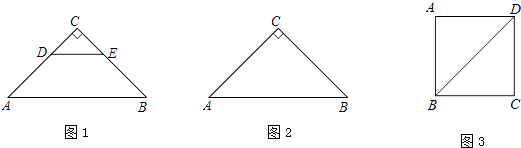
��1���������ⲹȫͼ2��
����֤��AD=BE����AD��BE��
����CM��DE������ΪM�����õ�ʽ��ʾ���߶�CM��AE��BE֮���������ϵ��
��2����ͼ3��������ABCD�߳�Ϊ ![]() ������P����PD=1���ҡ�BPD=90�㣬��ֱ��д����A��BP�ľ��룮
������P����PD=1���ҡ�BPD=90�㣬��ֱ��д����A��BP�ľ��룮
���𰸡�
��1��
�⣺���������ⲹȫͼ2������ͼ��һ����ʾ��

��֤�����ߡ�ACD+��DCB=��ACB=90�㣬��BCE+��DCB=��DCE=90�㣬
���ACD=��BCE��
�ߡ�ABC�͡�CDE���ǵ���ֱ�������Σ�
��AC=BC��DC=EC��
�ڡ�ADC�͡�BEC�У���  ��
��
���ADC�ա�BEC��SAS����
��AD=BE����BEC=��ADC��
�ߵ�A��D��E��ͬһֱ���ϣ���CDE�ǵ���ֱ�������Σ�
���CDE=��CED=45�㣬��ADC=180�㩁��CDE=135�㣬
���AEB=��BEC����CED=135�㩁45��=90�㣬
��AD��BE��
���������⻭��ͼ�Σ���ͼ��������ʾ��

��S��ABC+S��EBC=S��CAE+S��EAB��
�� ![]() ACBC+
ACBC+ ![]() BECM=
BECM= ![]() AE��CM+BE����
AE��CM+BE����
��AC2��AEBE=CM��AE��BE����
�ߡ�CDEΪ����ֱ�������Σ�
��DE=2CM��
��AE��BE=2CM
��2��
�⣺�������⻭��ͼ�Σ�������

����AB= ![]() ��DP=1��BD=
��DP=1��BD= ![]() AB=
AB= ![]()
�ɹ��ɶ����ã�BP= ![]() =3��
=3��
��ϣ�1���۵Ľ��ۿ�֪��
AM= ![]() =
= ![]() =1��
=1��
�ʵ�A��BP�ľ���Ϊ1
����������1���ٸ�����ת�����Ի���ͼ���ɡ�ACD����BCE�����DCB����ɵó���ACD=��BCE���ɡ�ABC�͡�CDE���ǵ���ֱ�������οɵó�AC=BC��DC=EC�����ȫ�������ε��ж�����SAS���ɵó���ADC�ա�BEC���Ӷ��ó�AD=BE�����ɡ�BCE=��ADC=135�㣬��CED=45�㼴�ɵó���AEB=90�㣬��֤��AD��BE�����������⻭��ͼ�Σ��������ͼ�ε����Ϊ���������ε�����Ϳ���AE��BEȥ��ʾCM����2���������⻭��ͼ�Σ����գ�1���۵Ľ��ۣ��������ݼ��ɵó����ۣ�
�����㾫����������Ĺؼ������������ֱ�������ε����֪ʶ�����յ���ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣮


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������У�����֤����ABD�ա�ACD���ǣ� ��.

A.BD=DC�� AB=AC B.��ADB=��ADC��BD=DC
C.��B=��C����BAD=��CAD D. ��B=��C��BD=DC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ�����⣺̽������y= ![]() x2+
x2+ ![]() ��ͼ�������ʣ�
��ͼ�������ʣ�
С������ѧϰ�����ľ��飬�Ժ���y= ![]() x2+
x2+ ![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1������y= ![]() x2+
x2+ ![]() ���Ա���x��ȡֵ��Χ��
���Ա���x��ȡֵ��Χ��
��2���±���y��x�ļ����Ӧֵ��
x | �� | ��3 | ��2 | ��1 | �� | �� |
|
| 1 | 2 | 3 | �� |
y | �� |
|
| �� | �� | �� |
|
|
|
| m | �� |
��m��ֵ��
��3����ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣮��������ĵ㣬�����ú�����ͼ�� 
��4����һ��̽�����֣��ú���ͼ���ڵ�һ�����ڵ���͵�������ǣ�1�� ![]() ������Ϻ�����ͼ��д���ú������������ʣ�һ�����ɣ� ��
������Ϻ�����ͼ��д���ú������������ʣ�һ�����ɣ� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н����ֶ�ij��ʵʩ����������ƶ����Ϊij���С�С������ͼ���ҹ�30�����ƻ���ֳ��ͼ�鲻����2000������ֲ��ͼ�鲻����1600������֪�齨һ������ͼ��������ֳ��ͼ��80������ֲ��ͼ��50�����齨һ��С��ͼ��������ֳ��ͼ��30������ֲ��ͼ��60����
��1������������齨�����м��֣���д��������齨������
��2�����齨һ������ͼ���ҵķ�����2000Ԫ���齨һ��С��ͼ���ҵķ�����1500Ԫ�����ַ���������ͣ���ͷ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�CD��AB���ϵĸߣ�AC=4��BC=3��DB=![]()

��1����AD�ij���
��2����ABC��ֱ����������Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ�ÿ��С�����εĶ���и�㣬��ABC�Ķ�����ڸ���ϣ� 
��1����������ABC����ƽ��2����λ��õ��ġ�A1B1C1 �� �ٻ�������A1B1C1�Ƶ�B1����ʱ�뷽����ת90������õ��ġ�A2B1C2��
��2�����߶�B1C1��ת��B1C2�Ĺ����У���C1��������·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����ij����һ���Ź��ŵĽ���ͼ�������Ŷ���������������״�����������˵���ˮ��ľ��붼��1m�����ŵĿ��Ϊ10cm���Ŷ���ˮ�����������5m���Ŷ�������ϸ���һյ����ˮ��4m�ľ��۵ƣ��ְѹ��ŵĽ���ͼ����ƽ��ֱ������ϵ�У���ͼ��2������ 
��1�������ߵĽ���ʽ��
��2����յ���۵�P1��P2֮���ˮƽ���룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD=��CAE=90�㣬AB=AD��AE=AC��AF��CB������ΪF��
��1����֤����ABC�ա�ADE��
��2������FAE�Ķ�����
��3����֤��CD=2BF+DE��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC=2����BAC=45�㣬��AEF���ɡ�ABC�Ƶ�A����ʱ�뷽����ת�õ��ģ�����BE��CF�ཻ�ڵ�D�� 
��1����֤��BE=CF��
��2�����ı���ABDFΪ����ʱ����CD�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com