
分析 (1)根据高斯求和公式即可求解;
(2)根据待定系数法得到月销售额y(万元)与月数x之间的函数关系式,根据今年9、10两个月的销售额正好等于开业初n个月的累计销售额,列出方程求解即可.
解答 解:(1)1+2+3+…+(n-1)+n=$\frac{n(n+1)}{2}$;
(2)设月销售额y(万元)与月数x之间的函数关系式为y=k(x+1)+b,依题意有
$\left\{\begin{array}{l}{k+2k+…+11k+12k=732}\\{k+2k+…+23k+24k=1752}\end{array}\right.$,
即$\left\{\begin{array}{l}{66k+12b=732}\\{12×23k+24b=1752}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=50}\end{array}\right.$.
则y=2(x-1)+50=2x+48,
至今年9月初,即x=24时,y=96(万元),
故今年9,10月共销售:96×(1+25%)+96×(1+25%)2=270(万元),
开业初几个月的累计销售额为50n+$\frac{n(n-2)}{2}$×2=n2+49n,
则n2+49n-270=0,
解得n1=5,n2=-54(舍去).
故n的值为5.
故答案为:$\frac{n(n+1)}{2}$.
点评 考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
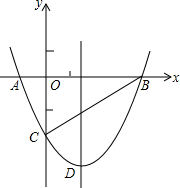 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
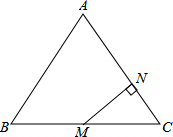 如图,在△ABC中,AB=AC=5cm,BC=6cm,M为BC中点,MN⊥AC,垂足为N,
如图,在△ABC中,AB=AC=5cm,BC=6cm,M为BC中点,MN⊥AC,垂足为N,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
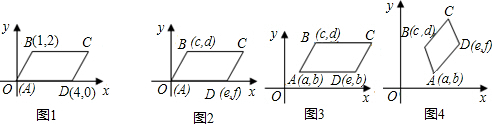
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 人数 | 3 | 4 | 2 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
| A. | 85和82.5 | B. | 85.5和85 | C. | 85和85 | D. | 85.5和80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com