
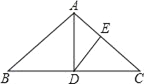
【题目】如图,已知AD是等腰△ABC底边上的高,且tanB=![]() .AC上有一点E,满足AE:CE=2:3.那么tan∠ADE的值是_____.
.AC上有一点E,满足AE:CE=2:3.那么tan∠ADE的值是_____.
【答案】![]()
【解析】
解:作EF⊥AD于F,根据△ABC为等腰三角形可得∠B=∠C,从而求出tanC= tanB=![]() ,设AD=3t,DC=4t,利用勾股定理求出AC=5t,再根据AE:CE=2:3,进而表示出AE=2t,根据平行得到△AEF∽△ACD,再根据相似的图形对应边成比例表示出FD,EF,进而在Rt△FDE,进而可得tan∠ADE.
,设AD=3t,DC=4t,利用勾股定理求出AC=5t,再根据AE:CE=2:3,进而表示出AE=2t,根据平行得到△AEF∽△ACD,再根据相似的图形对应边成比例表示出FD,EF,进而在Rt△FDE,进而可得tan∠ADE.
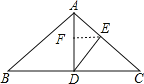
解:作EF⊥AD于F,如图,
∵△ABC为等腰三角形,AD为高,
∴∠B=∠C,
∵tanB=![]()
∴tanC= tanB=![]() =
=![]()
∴可设AD=3t,DC=4t,
∴AC=![]() =5t
=5t
∵AE:CE=2:3,
∴AE=2t,
∵EF⊥AD,AD是BC边上的高
∴EF∥CD,
∴△AEF∽△ACD,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() =
=![]()
∴EF=![]() t,AF=
t,AF=![]() t
t
∴FD=AD-AF= AF=![]() t,
t,
在Rt△DEF中,
tan∠FDE=![]() =
=![]()
∴tan∠ADE=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
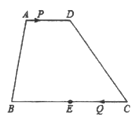
【题目】如图,在四边形![]() 中,
中,![]() ,
, ![]() 是
是![]() 的中点.点
的中点.点![]() 以每秒1个单位长度的速度从点
以每秒1个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动;点
运动;点![]() 同时以每秒3个单位长度的速度从 点
同时以每秒3个单位长度的速度从 点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.点
运动.点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动.当运动时间
也随之停止运动.当运动时间![]() 秒时,以点
秒时,以点![]() 为顶点的四边形是平行四边形.则
为顶点的四边形是平行四边形.则![]() 的值为_________.
的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
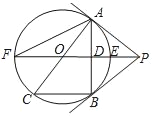
【题目】如图,PB为⊙O的切线,点B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF,
(1)求证:直线PA为⊙O的切线;
(2)若BC=6,tan∠F=![]() ,求cos∠ACB的值.
,求cos∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD的四个内角的平分线分别相交于点E、F、G、H,连接AC.若EF=2,FG=GC=5,则AC的长是( )

A. 12 B. 13 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
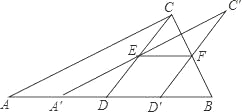
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装有红、黄、蓝三种颜色的球(除颜色以外,其余都相同),其中红球2个,黄球2个,从中随机摸出一个球是蓝色球的概率为![]() .
.
(1)求袋子里蓝色球的个数;
(2)甲、乙两人分别从袋中摸出一个球(不放回),求摸出的两个球中一个是红球一个是黄球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验初中组织了“英语手抄报”征集活动,现从中随机抽取部分作品,按A、B、C、D四个等级进行评价,并根据统计结果绘制了如下两幅不完整的统计图.
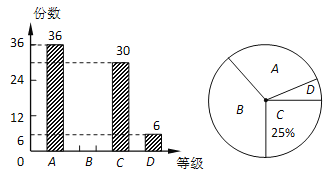
(1)抽取了_____份作品;
(2)此次抽取的作品中等级为B的作品有______份,并补全条形统计图;
(3)若该校共征集到600份作品,请估计等级为A的作品约有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
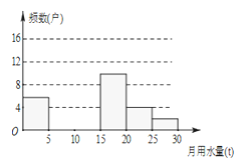
【题目】八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | m | 0.24 |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | n |
60≤x<70 | 2 | 0.04 |
请解答以下问题:
(1)求出吗、M,n的值,并把频数分布直方图补充完整;
(2)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com