[题目]如图.△ABC中.∠BAC＝108°.AD⊥BC于D.且AB+BD＝DC.则∠C的大小是( )A.20°B.24°C.30°D.36° 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，△ABC中，∠BAC＝108°，AD⊥BC于D，且AB+BD＝DC，则∠C的大小是（　　）

A.20°B.24°C.30°D.36°

【答案】B

【解析】

在DC上取DE＝DB．连接AE，在Rt△ABD和Rt△AED中，BD＝ED，AD＝AD．证明△ABD≌△AED（SAS）即可求解．

解：如图，在DC上取DE＝DB，连接AE．

在△ABD和△AED中，

，

∴Rt△ABD≌Rt△AED（SAS）．

∴AB＝AE，∠B＝∠AED．

又∵AB+BD＝DC，

∴EC＝DC﹣DE＝DC﹣BD＝(AB+BD)﹣BD＝AB＝AE，

即EC＝AE，

∴∠C＝∠CAE，

∴∠B＝∠AED＝2∠C，

又∵∠B+∠C＝180°﹣∠BAC＝72°，

∴3∠C＝72°，

∴∠C＝24°，

故选：B．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】小东家与学校之间是一条笔直的公路，早饭后，小东步行前往学校，途中发现忘带画板，停下给妈妈打电话，妈妈接到电话后，带上画板马上赶往学校，同时小东沿原路返回，两人相遇后，小东立即赶往学校，妈妈沿原路返回，16min时到家，假设小东始终以100m/min的速度步行，两人离家的距离y(单位：m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示：

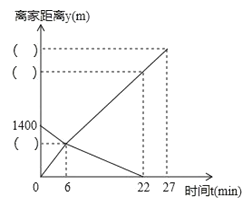
（1）小东打电话时，他离家_________m；

（2）填上图中空格相应的数据_________，_________，_________；

（3）小东和妈妈相遇后，妈妈回家的速度为_________m/min；

（4）_________min时，两人相距700m．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，，点在点的右侧，，的平分线交于点（不与，点重合），．设．

（1）若点在点的左侧，求的度数（用含的代数式表示）

（2）将（1）中的线段沿方向平移，当点移动到点右侧时，请画出图形并判断的度数是否改变．若改变，请求出的度数（用含的代数式表示）；若不变，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】我市某中学举行“中国梦校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如图所示．

（1）根据图示填写下表；

	平均数（分）	中位数（分）	众数（分）
初中部		85
高中部	85		100

（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；

（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．

【答案】（1）

	平均数（分）	中位数（分）	众数（分）
初中部	85	85	85
高中部	85	80	100

（2）初中部成绩好些（3）初中代表队选手成绩较为稳定

【解析】解：（1）填表如下：

	平均数（分）	中位数（分）	众数（分）
初中部	85	85	85
高中部	85	80	100

（2）初中部成绩好些。

∵两个队的平均数都相同，初中部的中位数高，

∴在平均数相同的情况下中位数高的初中部成绩好些。

（3）∵，

，

∴＜，因此，初中代表队选手成绩较为稳定。

（1）根据成绩表加以计算可补全统计表．根据平均数、众数、中位数的统计意义回答。

（2）根据平均数和中位数的统计意义分析得出即可。

（3）分别求出初中、高中部的方差比较即可。　

【题型】解答题
【结束】
21

【题目】受天气的影响，某超市鸡蛋供应紧张，需每天从外地调运鸡蛋1200斤，超市决定从甲、乙两个大型养殖场调运鸡蛋，已知从甲养殖场每天至少要调出300斤，从两养殖场调运鸡蛋到超市的路程和运费如下表：

	到超市的路程千米	运费元斤千米
甲养殖场	200
乙养殖场	140

设从甲养殖场调运鸡蛋x斤，总运费为W元，试写出W与x的函数关系式；

若某天计划从乙养殖场调运700斤鸡蛋，则总运费为多少元？

请你帮助超市设计一个调运方案，使得每天调运鸡蛋的总运费最低？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】直线MN与直线PQ垂直相交于O，点A在直线PQ上运动，点B在直线MN上运动．

（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．

（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．

（3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如果关于x的一次函数y＝（a+1）x+（a﹣4）的图象不经过第二象限，且关于x的分式方程有整数解，那么整数a值不可能是（）

A. 0B. 1C. 3D. 4

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H（A、H、B在一条直线上），并新修一条路CH，测得CB＝3千米，CH＝2.4千米，HB＝1.8千米．

（1）问CH是否为从村庄C到河边的最近路？（即问：CH与AB是否垂直？）请通过计算加以说明；

（2）求原来的路线AC的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图（1），在矩形ABCD中，AB=3，BC=4，连接BD．现将一个足够大的直角三角板的直角顶点P放在BD所在的直线上，一条直角边过点C，另一条直角边与AB所在的直线交于点G．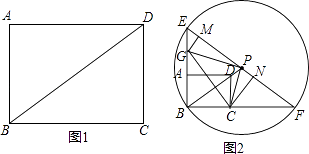

（1）是否存在这样的点P，使点P、C、G为顶点的三角形与△GCB全等？若存在，画出图形，并直接在图形下方写出BG的长．（如果你有多种情况，请用①、②、③、…表示，每种情况用一个图形单独表示，如果图形不够用，请自己画图）
（2）如图（2），当点P在BD的延长线上时，以P为圆心、PB为半径作圆分别交BA、BC延长线于点E、F，连EF，分别过点G、C作GM⊥EF，CN⊥EF，M、N为垂足．试探究PM与FN的关系．