
【题目】如图(1),在矩形ABCD中,AB=3,BC=4,连接BD.现将一个足够大的直角三角板的直角顶点P放在BD所在的直线上,一条直角边过点C,另一条直角边与AB所在的直线交于点G.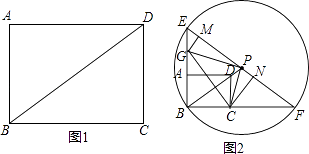
(1)是否存在这样的点P,使点P、C、G为顶点的三角形与△GCB全等?若存在,画出图形,并直接在图形下方写出BG的长.(如果你有多种情况,请用①、②、③、…表示,每种情况用一个图形单独表示,如果图形不够用,请自己画图)
(2)如图(2),当点P在BD的延长线上时,以P为圆心、PB为半径作圆分别交BA、BC延长线于点E、F,连EF,分别过点G、C作GM⊥EF,CN⊥EF,M、N为垂足.试探究PM与FN的关系.
【答案】
(1)解:存在点P,使点P、C、G为顶点的三角形与△GCB全等.
①若点G在线段AB上,如图①.
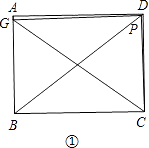
当BG=PC时,根据HL可得Rt△GBC≌Rt△CPG,
此时∠GCB=∠CGP,
∴PG∥BC,
∴∠GPC+∠PCB=90°.
∵∠GPC=90°,
∴∠PCB=90°,
∴点P在点D处,
∴BG=PC=DC=AB=3;
②若点G在线段AB的延长线上,如图②.
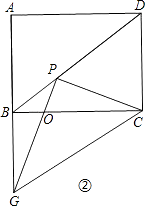
当BG=PC时,根据HL可得Rt△GBC≌Rt△CPG,
此时BC=PG,∠GCB=∠CGP,
∴OG=OC,OB=OP,
∴∠PBO=∠BPO= ![]() (180°﹣∠BOP),
(180°﹣∠BOP),
∠OCG=∠OGC= ![]() (180°﹣∠GOC).
(180°﹣∠GOC).
∵∠BOP=∠GOC,
∴∠PBO=∠OCG,
∴BD∥CG.
∵四边形ABCD是矩形,
∴AB∥DC,即BG∥DC,
∴四边形BGCD是平行四边形,
∴BG=CD=3;
③若点G在线段AB的反向延长线上,如图③.
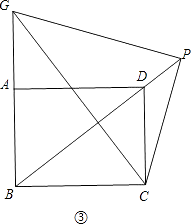
当PC=BC时,根据HL可得Rt△GBC≌Rt△GPC,
此时BG=PG,
∴点G、C在BP的垂直平分线上,
∴GC垂直平分BP,
∴∠BGC+∠GBD=90°.
∵∠CBD+∠GBD=90°,
∴∠BGC=∠CBD.
又∵∠GBC=∠BCD=90°,
∴△GCB∽△BDC,
∴ ![]() .
.
∵BC=4,CD=3,
∴ ![]() =
= ![]() ,
,
∴BG= ![]() ;
;
(2)解:如图2,
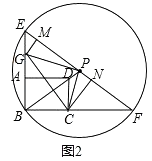
由(1)可知,此时△GBC≌△GPC,且BG=PG= ![]() ,BC=PC=4.
,BC=PC=4.
∵GM⊥EF,CN⊥EF,
∴∠GMP=∠PNC=90°,
∴∠MGP+∠GPM=90°.
∵∠GPC=90°,
∴∠GPM+∠NPC=90°,
∴∠MGP=∠NPC,
∴△PGM∽△CPN,
∴ ![]() .
.
∴ ![]() =
= ![]() ,即PM=
,即PM= ![]() CN.
CN.
∵PB=PF,∴∠F=∠PBC.
又∵∠FNC=∠BCD=90°,
∴△FNC∽△BCD,
∴ ![]() .
.
∵BC=4,DC=3,
∴ ![]() ,
,
∴FN= ![]() CN,
CN,
∴PM=FN.
【解析】(1)当BG=PC时,根据HL可得Rt△GBC≌Rt△CPG,此时∠GCB=∠CGP,得到PG∥BC,∠GPC+∠PCB=90°;由∠GPC=90°,∠PCB=90°,点P在点D处,得到BG=PC=DC=AB=3;(2)由(1)可知,此时△GBC≌△GPC,知道BG=PG,BC=PC的值,根据两角对应相等两三角形相似,得到△PGM∽△CPN,得到比例,得到△FNC∽△BCD,得到比例,得到PM=FN.
【考点精析】认真审题,首先需要了解圆心角、弧、弦的关系(在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】(2015随州)甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )

A. 4B. 3C. 2D. 1
【答案】B
【解析】
试题此题主要考查了一次函数的应用,读函数的图象的关键是理解横、纵坐标表示的意义,根据题意并结合横纵坐标的意义得出辆摩托车的速度,然后再分别分析,即可得出答案.
解:由图象可得:出发1小时,甲、乙在途中相遇,故①正确;
甲骑摩托车的速度为:120÷3=40(千米/小时),设乙开汽车的速度为a千米/小时,
则![]() ,
,
解得:a=80,
∴乙开汽车的速度为80千米/小时,
∴甲的速度是乙速度的一半,故④正确;
∴出发1.5小时,乙比甲多行驶了:1.5×(80﹣40)=60(千米),故②正确;
乙到达终点所用的时间为1.5小时,甲得到终点所用的时间为3小时,故③错误;
∴正确的有①②④,共3个,
故选:B.
考点:一次函数的应用.
【题型】单选题
【结束】
9
【题目】计算:![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有3个红球和1个白球,这些球除颜色外都相同.
(1)从中随机摸出1个球,记录颜色后放回,搅匀,再摸出1个球.摸出的两个球中,1个为红球,1个为白球的概率为;
(2)从中随机摸出1个球,记录颜色后不放回,再摸出1个球.求摸出的两个球中,1个为红球,1个为白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM.
(1)求证:AM与⊙O相切;
(2)若AM=3DM,BC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场统计了今年1﹣5月A、B两种品牌冰箱的销售情况,并将获得的数据绘制成如图折线统计图:
(1)根据图中数据填写表格.
(2)通过计算该商场这段时间内A、B两种品牌冰箱月销售量的方差,比较这两种品牌冰箱月销售量的稳定性.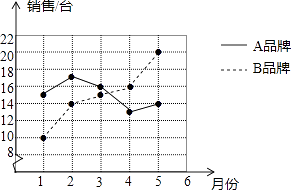
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为![]() ,
,![]() ,
,![]() ,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形
,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形![]() .
.
(1)画出三角形ABC和平移后![]() 的图形;
的图形;
(2)写出三个顶点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)求三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图2中,计算裁剪的角度∠BAD;
(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3 ![]() ,AE=3,求AF的长.
,AE=3,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com