
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3 ![]() ,AE=3,求AF的长.
,AE=3,求AF的长.
【答案】
(1)解:∵四边形ABCD是平行四边形
∴AD∥BC AB∥CD
∴∠ADF=∠CED ∠B+∠C=180°
∵∠AFE+∠AFD=180° ∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC
(2)解:∵四边形ABCD是平行四边形
∴AD∥BC CD=AB=4
又∵AE⊥BC
∴ AE⊥AD
在Rt△ADE中,DE= ![]()
∵△ADF∽△DEC
∴ ![]()
∴ ![]()
AF= ![]()
【解析】(1)根据平行四边形的性质,求出∠ADF=∠CED 、∠AFD=∠C ,根据两角相等两三角形相似,得到△ADF∽△DEC;(2)在Rt△ADE中,根据勾股定理求出DE的值,由(1)中的△ADF∽△DEC,得到比例,求出AF的值;


科目:初中数学 来源: 题型:
【题目】如图(1),在矩形ABCD中,AB=3,BC=4,连接BD.现将一个足够大的直角三角板的直角顶点P放在BD所在的直线上,一条直角边过点C,另一条直角边与AB所在的直线交于点G.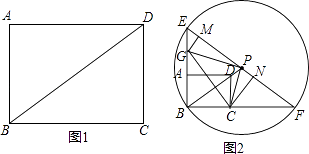
(1)是否存在这样的点P,使点P、C、G为顶点的三角形与△GCB全等?若存在,画出图形,并直接在图形下方写出BG的长.(如果你有多种情况,请用①、②、③、…表示,每种情况用一个图形单独表示,如果图形不够用,请自己画图)
(2)如图(2),当点P在BD的延长线上时,以P为圆心、PB为半径作圆分别交BA、BC延长线于点E、F,连EF,分别过点G、C作GM⊥EF,CN⊥EF,M、N为垂足.试探究PM与FN的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
请解答:(1)若![]() 的整数部分为
的整数部分为![]() ,小数部分为
,小数部分为![]() ,求
,求![]() 的值.
的值.
(2)已知:![]() ,其中
,其中![]() 是整数,且
是整数,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动.在一个不透明的口袋中有三个完全相同的小球,把它们分别标号1、2、3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为3万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.4万元,设可变成本平均每年增长的百分率为x.
(1)用含x的代数式表示第3年的可变成本为万元.
(2)如果该养殖户第3年的养殖成本为6.456万元,求可变成本平均每年增长的百分率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场的两个进球,提前一轮小组出线。如图,足球场上守门员在 ![]() 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 ![]() 处飞出(
处飞出( ![]() 在
在 ![]() 轴上),运动员孙可在距
轴上),运动员孙可在距 ![]() 点6米的
点6米的 ![]() 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点 ![]() ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)足球第一次落地点 ![]() 距守门员多少米?(取
距守门员多少米?(取 ![]() )
)
(3)孙可要抢到足球第二个落地点 ![]() ,他应从第一次落地点
,他应从第一次落地点 ![]() 再向前跑多少米?(取
再向前跑多少米?(取 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA切⊙O于A,AB⊥OP于B,若PO=8 cm,BO=2 cm,则PA的长为( ) 
A.16cm
B.48cm
C.6 ![]() cm
cm
D.4 ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是( )

A.106cmB.110cmC.114cmD.116cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com