
【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图2中,计算裁剪的角度∠BAD;
(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.


科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
【答案】(1)
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | 85 | 85 |
高中部 | 85 | 80 | 100 |
(2)初中部成绩好些(3)初中代表队选手成绩较为稳定
【解析】解:(1)填表如下:
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | 85 | 85 |
高中部 | 85 | 80 | 100 |
(2)初中部成绩好些。
∵两个队的平均数都相同,初中部的中位数高,
∴在平均数相同的情况下中位数高的初中部成绩好些。
(3)∵![]() ,
,
![]() ,
,
∴![]() <
<![]() ,因此,初中代表队选手成绩较为稳定。
,因此,初中代表队选手成绩较为稳定。
(1)根据成绩表加以计算可补全统计表.根据平均数、众数、中位数的统计意义回答。
(2)根据平均数和中位数的统计意义分析得出即可。
(3)分别求出初中、高中部的方差比较即可。
【题型】解答题
【结束】
21
【题目】受天气的影响,某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤,超市决定从甲、乙两个大型养殖场调运鸡蛋,已知从甲养殖场每天至少要调出300斤,从两养殖场调运鸡蛋到超市的路程和运费如下表:
到超市的路程 | 运费 | |
甲养殖场 | 200 | |
乙养殖场 | |
![]() 设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式;
设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式;
![]() 若某天计划从乙养殖场调运700斤鸡蛋,则总运费为多少元?
若某天计划从乙养殖场调运700斤鸡蛋,则总运费为多少元?
![]() 请你帮助超市设计一个调运方案,使得每天调运鸡蛋的总运费最低?
请你帮助超市设计一个调运方案,使得每天调运鸡蛋的总运费最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在矩形ABCD中,AB=3,BC=4,连接BD.现将一个足够大的直角三角板的直角顶点P放在BD所在的直线上,一条直角边过点C,另一条直角边与AB所在的直线交于点G.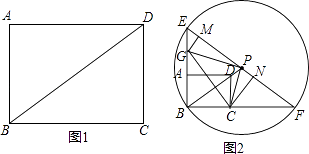
(1)是否存在这样的点P,使点P、C、G为顶点的三角形与△GCB全等?若存在,画出图形,并直接在图形下方写出BG的长.(如果你有多种情况,请用①、②、③、…表示,每种情况用一个图形单独表示,如果图形不够用,请自己画图)
(2)如图(2),当点P在BD的延长线上时,以P为圆心、PB为半径作圆分别交BA、BC延长线于点E、F,连EF,分别过点G、C作GM⊥EF,CN⊥EF,M、N为垂足.试探究PM与FN的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,AC与BD相交于0,AE⊥BD于E,CF⊥BD于F,则图中的全等三角形共( )

A. 5对B. 6对C. 7对D. 8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装着5个完全相同的小球,分别标有数字0,1,,2,-1,-2,从袋中随机取出一个小球。
(1)随机地从布袋中摸出一个小球,则摸出的球上数字为正数的概率为
(2)若第一次从布袋中随机摸出一个小球,设记下的数字为x,再将此球放回盒中,第二次再从布袋中随机抽取一张,设记下的数字为y,记M(x,y),请用画树状图或列表法列举出点M所有可能的坐标,并求点M位于第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
请解答:(1)若![]() 的整数部分为
的整数部分为![]() ,小数部分为
,小数部分为![]() ,求
,求![]() 的值.
的值.
(2)已知:![]() ,其中
,其中![]() 是整数,且
是整数,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动.在一个不透明的口袋中有三个完全相同的小球,把它们分别标号1、2、3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com