
【题目】已知抛物线y=(m﹣2)x2+2mx+m+3与x轴有两个交点.
(1)求m的取值范围;
(2)当m取满足条件的最大整数时,求抛物线与x轴有两个交点的坐标.
【答案】(1)m的取值范围是:m<6且m≠2.(2)抛物线与x轴有两个交点的坐标是:(﹣2,0),(![]() ,0).
,0).
【解析】
试题分析:(1)根据抛物线y=(m﹣2)x2+2mx+m+3与x轴有两个交点时,可知(m﹣2)x2+2mx+m+3=0时,△>0且m﹣2≠0,从而可以解答本题;
(2)根据第一问求得的m的取值范围,可以得到m的最大整数,从而可以求得抛物线与x轴有两个交点的坐标.
试题解析:(1)∵抛物线y=(m﹣2)x2+2mx+m+3与x轴有两个交点,
∴y=0时,(m﹣2)x2+2mx+m+3=0,则△=(2m)2﹣4×(m﹣2)×(m+3)>0,m﹣2≠0,
解得m<6且m≠2.即m的取值范围是:m<6且m≠2.
(2)∵m<6且m≠2,∴m满足条件的最大整数是m=5.
∴y=3x2+10x+8.当y=0时,3x2+10x+8=0.解得![]() .
.
即抛物线与x轴有两个交点的坐标是:(﹣2,0),(![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】长红枣是地方特产,色泽红艳,酥脆甘甜,营养丰富,有着较高的滋补和药用价值,被誉为“天然维生素丸”.某网店以a元一包的价格购进500包长红枣,加价20%卖出400包以后,剩余每包比进价降低b元后全部卖出,则可获得利润_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为﹣10,B点对应的数为90. ![]()
(1)请写出与AB两点距离相等的M点对应的数;
(2)现在有一只电子蚂蚁P从B点出发时,以5个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以3个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,你知道对应的数是多少吗?
(3)若当电子蚂蚁P从B点出发时,以5个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以3个单位/秒的速度向左运动,经过多长的时间两只电子蚂蚁在数轴上相距30个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中,不正确的是( )
A.a+(b+c﹣d)=a+b+c﹣d
B.a﹣(b﹣c+d)=a﹣b+c﹣d
C.a﹣b﹣(c﹣d)=a﹣b﹣c﹣d
D.a+b﹣(﹣c﹣d)=a+b+c+d
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,点A,B,C,D均在格点上,点E,F分别为线段BC,DB上的动点,且BE=DF.
(1)如图①所示,当BE=![]() 时,计算AE+AF的值等于____;
时,计算AE+AF的值等于____;
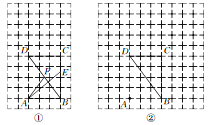
(2)当AE+AF取最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段AE,AF,并简要说明点E和点F的位置是如何找到的(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在同心圆中,大圆的弦AB交小圆于C、D两点.
(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+2的图象与x轴的正半轴交于点A,与y轴的正半轴交交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.
(1)求这个二次函数的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;
(3)设(2)中平移后所得二次函数图象与y轴的交点为B1,顶点为D1.点P在平移后的二次函数图象上,且满足△PBB1的面积是△PDD1面积的2倍,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com