
【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
(1)从小刚家到该景区乘车一共用了多少时间?
(2)求线段AB对应的函数解析式;
(3)小刚一家出发2.5小时时离目的地多远?

【答案】(1)4h;(2)y=120x﹣40(1≤x≤3);(3)小刚一家出发2.5小时时离目的地120km远.
【解析】试题分析:(1)观察图形即可得出结论;(2)设AB段图象的函数表达式为y=kx+b,将A、B两点的坐标代入,运用待定系数法即可求解;(3)先将x=2.5代入AB段图象的函数表达式,求出对应的y值,进一步即可求解.
试题解析:(1)从小刚家到该景区乘车一共用了4h时间;
(2)设AB段图象的函数表达式为y=kx+b.
∵A(1,80),B(3,320)在AB上,
∴![]() ,
,
解得![]() .
.
∴y=120x﹣40(1≤x≤3);
(3)当x=2.5时,y=120×2.5﹣40=260,
380﹣260=120(km).
故小刚一家出发2.5小时时离目的地120km远.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
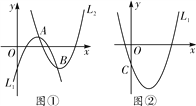
【题目】如图①,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上(点A与点B不重合),我们把这样的两抛物线L1、L2称为“伴随抛物线”,可见一条抛物线的“伴随抛物线”可以有多条.
(1)抛物线L1:y=-x2+4x-3与抛物线L2是“伴随抛物线”,且抛物线L2的顶点B的横坐标为4,求抛物线L2的表达式;
(2)若抛物线y=a1(x-m)2+n的任意一条“伴随抛物线”的表达式为y=a2(x-h)2+k,请写出a1与a2的关系式,并说明理由;
(3)在图②中,已知抛物线L1:y=mx2-2mx-3m(m>0)与y轴相交于点C,它的一条“伴随抛物线”为L2,抛物线L2与y轴相交于点D,若CD=4m,求抛物线L2的对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解九年级学生的身体素质测试情况,随机抽取了该市九年级部分学生的身体素质测试成绩作为样本,按A(优秀),B(良好),C(合格),D(不合格)四个等级进行统计,并将统计结果绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题:

(1)此次共调查了多少名学生?
(2)将条形统计图补充完整,并计算扇形统计图中“A”部分所对应的圆心角的度数.
(3)该市九年级共有8000名学生参加了身体素质测试,估计测试成绩在良好以上(含良好)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A. OA=OC,OB=ODB. OA=OC,AB∥CD
C. AB=CD,OA=OCD. ∠ADB=∠CBD,∠BAD=∠BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据.
水笔支数 | 4 | 6 | 8 | 7 | 5 |
需要更换的笔芯个数x | 7 | 8 | 9 | 10 | 11 |
设x表示水彩笔在使用期内需要更换的笔芯个数,y表示每支水彩笔在购买笔芯上所需要的费用(单位:元),n表示购买水彩笔的同时购买的笔芯个数.
(1)若x=9,n=7,则y= ;若x=7,n=9,则y= ;
(2)若n=9,用含x的的代数式表示y的取值;
(3)假设这30支笔在购买时,每支笔同时购买9个笔芯,或每支笔同时购买10个笔芯,分别计算这30支笔在购买笔芯时所需的费用,以费用最省作为选择依据,判断购买一支水彩笔的同时应购买9个还是10个笔芯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).

(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=![]() 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是 、 ;
(2)当点P运动的路程x=4时,△ABP的面积为y= ;
(3)求AB的长和梯形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于两个两位数m和n,将其中任意一个两位数的十位上的数字和个位上的数字分别放置于另一个两位数十位上数字与个位上的数字之间和个位上的数字的右边,就可以得到两个新四位数,把这两个新四位数的和与11的商记为F(m,n)。例如:当m=36,n=10时,将m十位上的3放置n中1与0之间,将m个位上的6位置于n中0的右边,得到1306.将n个十位上的1放置于m中3和6之间,将n个位上的0放置于m中6的右边,得到3160。这两个新四位数的和为1306+3160=4466,4466÷11=406,所以F(36,10)=406。
(1)计算:F(20,18);
(2)若a=10+x,b=10y+8(0≤x≤9,1≤y≤9,x,y都是自然数)。当150 F(a,36)+ F(b,49)=62767时,求F(5a,b)的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com