
【题目】如图①,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上(点A与点B不重合),我们把这样的两抛物线L1、L2称为“伴随抛物线”,可见一条抛物线的“伴随抛物线”可以有多条.
(1)抛物线L1:y=-x2+4x-3与抛物线L2是“伴随抛物线”,且抛物线L2的顶点B的横坐标为4,求抛物线L2的表达式;
(2)若抛物线y=a1(x-m)2+n的任意一条“伴随抛物线”的表达式为y=a2(x-h)2+k,请写出a1与a2的关系式,并说明理由;
(3)在图②中,已知抛物线L1:y=mx2-2mx-3m(m>0)与y轴相交于点C,它的一条“伴随抛物线”为L2,抛物线L2与y轴相交于点D,若CD=4m,求抛物线L2的对称轴.
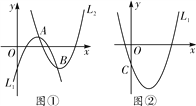
【答案】(1)y=(x-4)2-3(2)伴随抛物线的顶点不重合,∴m≠h,∴a1=-a2(3)抛物线L2的对称轴为x=±2.
【解析】试题分析:(1)先分别求得点A、点B的坐标,然后再利用待定系数法进行求解即可;
(2)根据:抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上,可以列出两个方程,相加可得:(a1+a2 )(m-h)2=0,可得a1=-a2;
(3)易得抛物线L1的顶点坐标为(1,-4m),设抛物线L2的顶点的横坐标为h,则其纵坐标为mh2-2mh-3m,则有抛物线L2的表达式为y=-mx2+2mhx-2mh-3m,从而得点D的坐标为(0,-2mh-3m),再根据点C的坐标为(0,-3m),从而可得|(-2mh-3m)-(-3m)|=4m,解得h=±2,从而得抛物线L2的对称轴为x=±2.
试题解析:(1)由y=-x2+4x-3可得A的坐标为(2,1),
将x=4代入y=-x2+4x-3,得y=-3,∴B的坐标为(4,-3),
设抛物线L2的解析式为y=a(x-4)2-3; 将(2,1)代入y=a(x-4)2-3,
得1=a(2-4)2-3,解得a=1,
∴抛物线L2的表达式为y=(x-4)2-3;
(2)a1=-a2,理由如下:
∵抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上,
∴可列方程组: 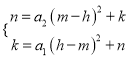 ,
,
整理,得(a1+a2)(m-h)2=0,
∵伴随抛物线的顶点不重合,∴m≠h,∴a1=-a2;
(3)抛物线L1:y=mx2-2mx-3m的顶点坐标为(1,-4m),
设抛物线L2的顶点的横坐标为h,则其纵坐标为mh2-2mh-3m,
∴抛物线L2的表达式为y=-m(x-h)2+mh2-2mh-3m,
化简得,y=-mx2+2mhx-2mh-3m,
所以点D的坐标为(0,-2mh-3m),
又点C的坐标为(0,-3m),
可得|(-2mh-3m)-(-3m)|=4m, 解得h=±2,
∴抛物线L2的对称轴为x=±2.


科目:初中数学 来源: 题型:
【题目】节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水![]() 与滴水时间
与滴水时间![]() 的关系用可以显示水量的容器做如图
的关系用可以显示水量的容器做如图![]() 的试验,并根据试验数据绘制出如图
的试验,并根据试验数据绘制出如图![]() 的函数图象,结合图象解答下列问题.
的函数图象,结合图象解答下列问题.
(![]() )容器内原有水多少升.
)容器内原有水多少升.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.


查看答案和解析>>
科目:初中数学 来源: 题型:
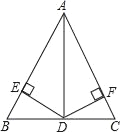
【题目】如图,在△ABC中,AD平分∠BAC交BC于D,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:AB=AC;
(2)若DC=4,∠DAC=30°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读学习】 刘老师提出这样一个问题:已知α为锐角,且tanα=![]() ,求sin2α的值.
,求sin2α的值.
小娟是这样解决的:
如图1,在⊙O中,AB是直径,点C在⊙O上,∠BAC=α,所以∠ACB=90°,tanα=![]() =
=![]() .
.
易得∠BOC=2α.设BC=x,则AC=3x,则AB=![]() x.作CD⊥AB于D,求出CD= (用含x的式子表示),可求得sin2α=
x.作CD⊥AB于D,求出CD= (用含x的式子表示),可求得sin2α=![]() = .
= .
【问题解决】
已知,如图2,点M、N、P为圆O上的三点,且∠P=β,tanβ =![]() ,求sin2β的值.
,求sin2β的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点E为BC边上一点,AE和BD交于点F,已知△ABF的面积等于 6,△BEF的面积等于4,则四边形CDFE的面积等于___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为-3,0,1,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M,点N的距离相等,那么x的值是______________;
(2)数轴上是否存在点P,使点P到点M,点N的距离之和是5?若存在,请直接写出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,C是⊙O上的一点,连结AC并延长至D,使CD=AC,连结BD,作CE⊥BD,垂足为E。
(1)线段AB与DB的大小关系为 ,请证明你的结论;
(2)判断CE与⊥⊙O的位置关系,并证明;
(3)当△CED与四边形ACEB的面积比是1:7时,试判断△ABD的形状,并证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
(1)从小刚家到该景区乘车一共用了多少时间?
(2)求线段AB对应的函数解析式;
(3)小刚一家出发2.5小时时离目的地多远?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com