练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，Rt△OAB的直角边OB在x轴上，反比例函数y=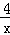在第一象限的图象经过其顶点A，点D为斜边OA的中点，另一个反比例函数y1=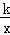在第一象限的图象经过点D，则k的值为（　　）

    　 A． 1 B． 2 C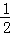．  D． 无法确定


    A

    考点： 反比例函数图象上点的坐标特征． 

    分析： 过点D作DE⊥x轴于点E，由点D为斜边OA的中点可知DE是△AOB的中位线，设A（x，），则D（，），再求出k的值即可．

    解答： 解：过点D作DE⊥x轴于点E，

    ∵点D为斜边OA的中点，点A在反比例函数y=上，

    ∴DE是△AOB的中位线，

    设A（x，），则D（，），

    ∴k=•=1．

    故选A．

    点评： 本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    ﹣22﹣（﹣2）2﹣23×（﹣1）2013

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列说法①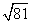的算术平方根是9 ，②将8450亿元用科学记数法表示为8.45×1011元  ，③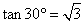，④正八边形中心角是45°，⑤若一次函数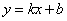的图象不经过第三象限,则 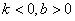，其中正确的有（  ）

    A．0个    B．1个      C．2个   D．3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，PA为⊙O的切线，点A为切点，直线PO交⊙O于点E，F，过点A作PO的垂线AB，垂足为点C，交⊙O于点B，延长BO与⊙O交于点D，连接AD，连接BE，

    （1）求证：直线PB为⊙O的切线，

    （2）试探究线段EF，OP，OC之间的数量关系，并加以证明，

    （3）若BC=9，tan∠E=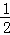，求cos∠ADB的值和线段PE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，E，F，G，H分别是OA，OB，OC，OD的中点，已知四边形EFGH的面积是3，则四边形ABCD的面积是（　　）

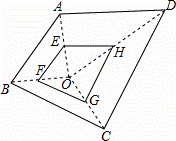
    　 A． 6 B． 9 C． 12 D． 18

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：=　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，足球上守门员在O处开出一高球．球从离地面1米的A处飞出（A在y轴上），把球看成点．其运行的高度y（单位：m）与运行的水平距离x（单位：m）满足关系式y=a（x﹣6）2+h．

    （1）①当此球开出后．飞行的最高点距离地面4米时．求y与x满足的关系式．

    ②在①的情况下，足球落地点C距守门员多少米？（取4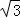≈7）

    ③如图所示，若在①的情况下，求落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．求：站在距O带你6米的B处的球员甲要抢到第二个落点D处的求．他应再向前跑多少米？（取2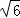=5）

    （2）球员乙升高为1.75米．在距O点11米的H处．试图原地跃起用头拦截．守门员调整开球高度．若保证足球下落至H正上方时低于球员乙的身高．同时落地点在距O点15米之内．求h的取值范围．

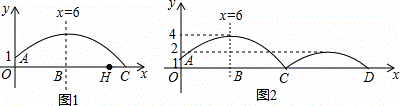
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，后求值：，再任选一个你喜欢的数x代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列哪个不等式组的解集在数轴上的表示如图所示

    A．            B．

    C．           D．

    查看答案和解析>>

    同步练习册答案