
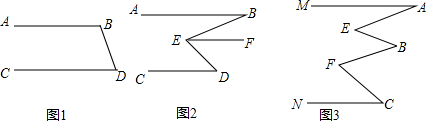
分析 (1)根据平行线的性质“两直线平行,同旁内角互补”将题补充完整,即可得出结论;
(2)根据平行线的性质“两直线平行,内错角相等”将题补充完整,即可得出结论;
(3)过点B作BQ∥MA,根据(2)的结论,即可证出∠A+∠B+∠C=∠E+∠F.
解答 解:(1)如图1所示:已知AB∥CD,∠ABD=115°,
根据两直线平行,同旁内角互补可得出:∠BDC的度数是65°.
故答案为:两直线平行,同旁内角互补;65°.
(2)如图2所示:已知AB∥CD,∠ABE=25°,∠EDC=40°,求∠BED的度数.
解:过点E作EF∥AB
∵AB∥CD(已知)∴EF∥CD(平行于同一条直线的两直线平行).
∵EF∥AB,EF∥CD
∴∠ABE=∠BEF,∠EDC=∠DEF(两直线平行,内错角相等).
∴∠BEF=25°,∠DEF=40°
即∠BED=65°.
故答案为:平行于同一条直线的两直线平行;两直线平行,内错角相等;65°.
(3)如图3所示:已知MA∥NC,试确定∠A、∠B、∠C和∠E、∠F的关系是∠A+∠B+∠C=∠E+∠F.
证明:在图3中过点B作BQ∥MA,如图所示.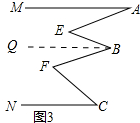
由(2)可知∠A+∠EBQ=∠E,∠C+∠FBQ=∠F,
∴∠A+∠EBQ+∠C+∠FBQ=∠E+∠F,
∵∠B=∠EBQ+∠FBQ,
∴∠A+∠B+∠C=∠E+∠F.
故答案为:∠A+∠B+∠C=∠E+∠F.
点评 本题考查了平行线的性质以及角的计算,解题的关键:(1)熟记“两直线平行,同旁内角互补”;(2)熟记“两直线平行,内错角相等”;(3)结合(2)的结论,通过角的计算得出结论.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找到相等(或互补)的角,再通过角的计算得出结论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
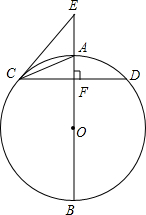 如图,已知AB为⊙O的直径,弦CD⊥AB,垂足为F,E为BA延长线上的一点,连接CE、CA,∠ECA=∠ACD.
如图,已知AB为⊙O的直径,弦CD⊥AB,垂足为F,E为BA延长线上的一点,连接CE、CA,∠ECA=∠ACD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
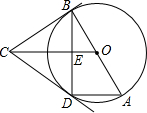 如图,已知AB是⊙O的直径,BC是⊙O的切线,B是切点,⊙O的弦AD∥OC.
如图,已知AB是⊙O的直径,BC是⊙O的切线,B是切点,⊙O的弦AD∥OC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
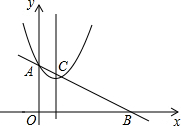 如图,在平面直角坐标系中,抛物线y=x2-2x+2交y轴于点A,直线AB交x轴正半轴于点B,交抛物线的对称轴于点C,若OB=2OA,则点C的坐标为(1,$\frac{3}{2}$).
如图,在平面直角坐标系中,抛物线y=x2-2x+2交y轴于点A,直线AB交x轴正半轴于点B,交抛物线的对称轴于点C,若OB=2OA,则点C的坐标为(1,$\frac{3}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com