
分析 (1)根据幂的乘方底数不变指数相乘,可得指数相的幂的乘积,根据积的乘方等于乘方的积,可得答案;
(2)根据同底数幂的乘法底数不变指数相加,可得积的乘方,根据积的乘方,可得答案;
(3)根据零次幂、负整数指数幂与正整数指数幂互为倒数,可得答案.
解答 解:(1)原式=(-3)3(a3)3(b4)3=(-3a3b4)3,
(2)原式=(-0.125)2012•(-8)2012•(-8)=[-0.125×(-8)]2012×(-8)=-8;
(3)原式=1×$\frac{1}{9}$=$\frac{1}{9}$,
故答案为:(-3a3b4),-8,$\frac{1}{9}$.
点评 本题考查了幂的乘方与积的乘方,熟记法则并根据法则计算是解题关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3ab^2}$和$\sqrt{3ab^2c}$ | B. | $\sqrt{12ab^3}$和$\sqrt{3ab}$ | C. | $\sqrt{ab}$和$\sqrt{{a}^{3}{b}^{5}}$ | D. | $\sqrt{\frac{b}{a}}$和$\sqrt{\frac{a}{b}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
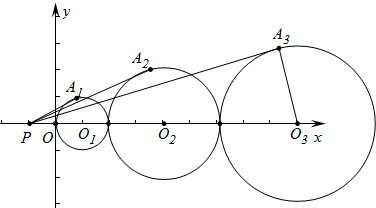 如图,点P(-1,0),以圆心在x轴正半轴上连续作圆,半径分别为1、2、3,过点P作圆的切线,切点分别为A1、A2、A3,则sin∠O3PA3=$\frac{3}{10}$.
如图,点P(-1,0),以圆心在x轴正半轴上连续作圆,半径分别为1、2、3,过点P作圆的切线,切点分别为A1、A2、A3,则sin∠O3PA3=$\frac{3}{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
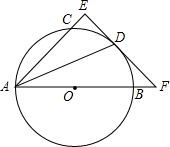 如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.
如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
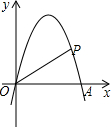 如图,在平面直角坐标系中,抛物线y=-x2+4x与x轴交于点O、A,点P在抛物线上,连结OP、AP,设点P的横坐标为m,△AOP的面积为S,若0<m<3,则S的取值范围是0<S≤8.
如图,在平面直角坐标系中,抛物线y=-x2+4x与x轴交于点O、A,点P在抛物线上,连结OP、AP,设点P的横坐标为m,△AOP的面积为S,若0<m<3,则S的取值范围是0<S≤8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
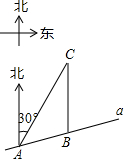 如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量,B位于A的北偏东75°方向,C位于B的正北方向,C位于A的北偏东30°方向,AB=8km.
如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量,B位于A的北偏东75°方向,C位于B的正北方向,C位于A的北偏东30°方向,AB=8km.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com