
【题目】(1)学校“圆周率”数学社团遇到这样一个题目:
如图1,在![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() ,求
,求![]() 的长.
的长.
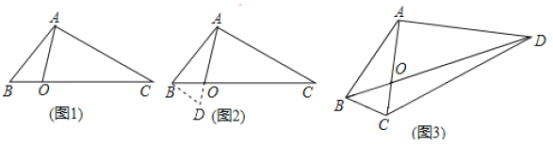
经过社团成员讨论发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() 就可以解决问题(如图2). 请回答:
就可以解决问题(如图2). 请回答:![]() _______,
_______,![]() ______;
______;
(2)请参考以上解决思路,解决问题:
如图3,在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长及四边形
的长及四边形![]() 的面积.
的面积.
【答案】(1)![]() ,10;(2)
,10;(2)![]() ,
,![]() .
.
【解析】
(1)根据平行线的性质可得出∠ADB=∠OAC=75°,结合∠BOD=∠COA可得出△BOD∽△COA,利用相似三角形的性质可求出OD的值,进而可得出AD的值,由三角形内角和定理可得出∠ABD=75°=∠ADB,由等角对等边可得出AB=AD=10,此题得解;(2)过点B作BE∥AD交AC于点E,同(1)可得出AE=10,在Rt△AEB中,利用勾股定理可求出BE的长度,再在Rt△CAD中,利用勾股定理可求出DC的长,此题得解;四边形ABCD的面积等于△ABC和△ADC的面积之和,利用以求的数据求解即可.
解:(1)∵BD∥AC,
∴∠ADB=∠OAC=75°.
∵∠BOD=∠COA,
∴△BOD∽△COA,
∴![]() .
.
又∵AO=8,
∴OD=![]() AO=2,
AO=2,
∴AD=AO+OD=10.
∵∠BAD=30°,∠ADB=75°,
∴∠ABD=180°-∠BAD-∠ADB=75°=∠ADB,
∴AB=AD=10.
故答案为:![]() ,10.
,10.
(2)过点B作BE∥AD交AC于点E,如图所示.
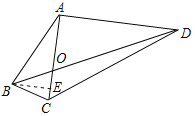
∵AC⊥AD,BE∥AD,
∴∠DAC=∠BEA=90°.
∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴![]()
∵BO:OD=1:4,
∴![]() .
.
∵AO=8,
∴EO=2,
∴AE=10.
∵∠ABC=∠ACB=75°,
∴∠BAC=30°,AB=AC,
又∵![]()
∴AB=2BE.
在Rt△AEB中,BE2+AE2=AB2,即102+BE2=(2BE)2,
解得:BE=![]() ,
,
∴AB=AC=![]() ,AD=
,AD=![]() .
.
在Rt△CAD中,AC2+AD2=CD2,
∴CD=![]() .
.
![]()
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某茶叶销售商计划将m罐茶叶按甲、乙两种礼品盒包装出售,其中甲种礼品盒每盒装4罐,每盒售价240元;乙种礼品盒每盒装6罐,每盒售价300元,恰好全部装完.已知每罐茶叶的成本价为30元,设甲种礼品盒的数量为x盒,乙种礼品盒的数量为y盒.
(1)当m=120时.
①求y关于x的函数关系式.
②若120罐茶叶全部售出后的总利润不低于3000元,则甲种礼品盒的数量至少要多少盒?
(2)若m罐茶叶全部售出后平均每罐的利润恰好为24元,且甲、乙两种礼品盒的数量和不超过69盒,求m的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一张盾构隧道断面结构图.隧道内部为以O为圆心,AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为1.6m,顶棚到路面的距离是6.4m,点B到路面的距离为4.0m.请求出路面CD的宽度.(精确到0.1m)
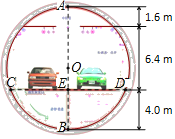
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交与A(1,0),B(﹣3,0)两点,顶点为D,交y轴于C.
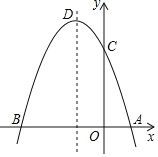
(1)求该抛物线的解析式.
(2)在抛物线的对称轴上是否存在着一点M使得MA+MC的值最小,若存在求出M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
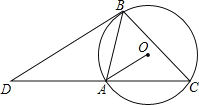
【题目】已知:如图,AB是⊙O的弦,∠OAB=45°,C是优弧AB上的一点,BD∥OA,交CA延长线于点D,连接BC.
(1)求证:BD是⊙O的切线;
(2)若AC=![]() ,∠CAB=75°,求⊙O的半径.
,∠CAB=75°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
⑴请你补全这个输水管道的圆形截面;
⑵若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com