
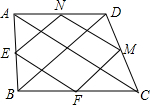
 在四边形ABCD中,连接对角线AC,BD,E、F、M、N分别是AB、BC、CD、AD的中点,连接EF、FM、MN、EN,下列条件中,能使四边形EFMN是菱形的是( )
在四边形ABCD中,连接对角线AC,BD,E、F、M、N分别是AB、BC、CD、AD的中点,连接EF、FM、MN、EN,下列条件中,能使四边形EFMN是菱形的是( )| A. | AB=BC | B. | AB⊥BC | C. | AC⊥BD | D. | AC=BD |
分析 首先根据三角形的中位线定理,可以证明所得四边形的两组对边分别和两条对角线平行,所得四边形的两组对边分别是两条对角线的一半,再根据平行四边形的判定就可证明该四边形是一个平行四边形,再根据所得四边形要成为菱形,则需有一组邻边相等,故对角线应满足相等即可.
解答 解:
∵E、F、M、N分别是AB、BC、CD、DA边上的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC,FM∥BD,FM=$\frac{1}{2}$BD,GN∥AC,GN=$\frac{1}{2}$AC,EN∥BD,EN=$\frac{1}{2}$BD.
∴EF∥MN,EF=MN,FM∥EN,FM=EN.
∴四边形EFMN是平行四边形,
∵AC=BD,
∴EF=EN,
∴四边形EFMN为菱形.
故选A.
点评 此题主要是对三角形的中位线定理的运用.
同时熟记此题中的结论:
顺次连接四边形各边中点所得四边形是平行四边形;
顺次连接对角线互相垂直的四边形各边中点所得四边形是矩形;
顺次连接对角线相等的四边形各边中点所得四边形是菱形;
顺次连接对角线垂直且相等的四边形各边中点所得四边形是正方形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 序号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 甲命中的环数(环) | 7 | 8 | 8 | 6 | 9 | 8 | 10 |
| 乙命中的环数(环) | 5 | 10 | 6 | 7 | 8 | 10 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a:b:c=1:$\sqrt{2}$:1 | B. | ∠A:∠B:∠C=3:4:5 | C. | (a+b)(a-b)=c2 | D. | ∠A:∠B:∠C=1:2:3 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:解答题
在平面直角坐标系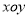 中,已知点
中,已知点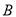 (-3,4)关于
(-3,4)关于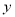 轴的对称点为
轴的对称点为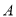 .
.
(1)直接写出 点的坐标;
点的坐标;
(2)求出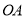 的长;
的长;
(3)设点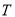 (
(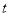 ,0)是
,0)是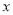 轴正半轴上的一个动点,当△ATO是等腰三角形时,求
轴正半轴上的一个动点,当△ATO是等腰三角形时,求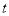 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com