Question

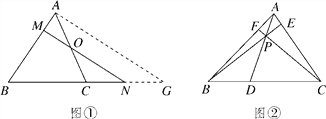
【题目】如图①所示，在△ABC中，点O是AC上一点，过点O的直线与AB，BC的延长线分别相交于点M，N.

【问题引入】

(1)若点O是AC的中点， ，求的值；

温馨提示：过点A作MN的平行线交BN的延长线于点G.

【探索研究】

(2)若点O是AC上任意一点(不与A，C重合)，求证： ；

【拓展应用】

(3)如图②所示，点P是△ABC内任意一点，射线AP，BP，CP分别交BC，AC，AB于点D，E，F.若， ，求的值．

Answer 1

【答案】（1）（2）证明见解析（3）

【解析】试题分析:(1)作AG∥MN交BN延长线于点G,证△ABG∽△MBN得,

即,同理可证△ACG∽△OCN得,结合AO=CO,得NG=CN,从而由进行求解,

(2)由,可知: ,

(3)由(2)可知,在△ABD中有, 在△ACD中有,

从而,因此可得: .

(1)解：过点A作MN的平行线交BN的延长线于点G.∵ON∥AG，∴＝.∵O是AC的中点，∴AO＝CO，∴NG＝CN.∵MN∥AG，∴＝，∴＝＝＝.

(2)证明：由(1)可知＝，＝，∴··＝··＝1.

(3)解：在△ABD中，点P是AD上一点，过点P的直线与AB，BD的延长线分别相交于点F，C.由(2)可得··＝1.在△ACD中，过点P的直线与AC，CD的延长线分别相交于点E，B.由(2)可得··＝1.∴··＝··，∴＝·＝×＝.