Question

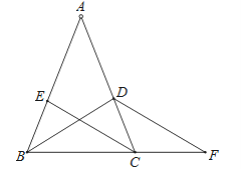
【题目】如图，已知点E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足.连接CD，且交OE于点F．

（1）求证：OE是CD的垂直平分线．

（2）若∠AOB=60°，求证：OE=4EF．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：（1）根据角平分线的性质得到ED=EC，证明Rt△ODE≌Rt△OCE，得到OD=OC，根据线段垂直平分线的判定定理证明结论；

（2）根据在直角三角形中，30°所对的直角边是斜边的一半解答即可．

试题解析：（1）证明：∵E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，

∴ED=EC，

在Rt△ODE和Rt△OCE中，

，

∴Rt△ODE≌Rt△OCE，

∴OD=OC，又ED=EC，

∴OE是CD的垂直平分线；

（2）∵∠AOB=60°，

∴∠BOE=30°，

∴OE=2DE，

∵ED⊥OB，OE⊥CD，∠BOE=30°，

∴∠FDE=30°，

∴DE=2EF，

∴OF：FE=3：1．

∴OE=4EF．