
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=![]() ,AB=3,求BD的长.
,AB=3,求BD的长.

【答案】(1)证明见解析;(2)1.
【解析】试题分析:(1)利用切线的性质和等腰三角形的性质可以得出∠DCE=∠E,进而得出答案;
(2)设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,利用勾股定理得出BD的长.
试题解析:(1)连接OC,∵CD是⊙O的切线,∴∠OCD=90°,∴∠ACO+∠DCE=90°,又∵ED⊥AD,∴∠EDA=90°,∴∠EAD+∠E=90°,∵OC=OA,∴∠ACO=∠EAD,故∠DCE=∠E,∴DC=DE;
(2)设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,在Rt△EAD中,∵tan∠CAB=![]() ,∴ED=
,∴ED=![]() AD=
AD=![]() (3+x),由(1)知,DC=
(3+x),由(1)知,DC=![]() (3+x),在Rt△OCD中,
(3+x),在Rt△OCD中,![]() ,则
,则![]() ,解得:
,解得:![]() (舍去),
(舍去),![]() ,故BD=1.
,故BD=1.



 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】将一条长为40cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于52cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于48cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
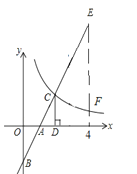
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A,B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②![]() ;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足.连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,求证:OE=4EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某房地产开发公司计划建![]() 、
、![]() 两种户型的住房共80套,该公司所筹资金不少于
两种户型的住房共80套,该公司所筹资金不少于![]() 万元,但不超过
万元,但不超过![]() 万元,且所筹资金全部用于建房,两种户型的建房的成本和售价如表:
万元,且所筹资金全部用于建房,两种户型的建房的成本和售价如表:
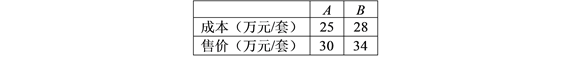
(![]() )该公司对这两种户型住房有哪几种方案?
)该公司对这两种户型住房有哪几种方案?
(![]() )该公司如何建房获利利润最大?
)该公司如何建房获利利润最大?
(![]() )根据市场调查,每套
)根据市场调查,每套![]() 型住房的售价不会改变,每套
型住房的售价不会改变,每套![]() 型住房的售价将会提高
型住房的售价将会提高![]() 万元
万元![]() ,且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?
,且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
①3+4×(﹣2);
②1﹣(2﹣3)2×(﹣2)3;
③|﹣9|÷3+(![]() ﹣
﹣![]() )×12+32;
)×12+32;
④2﹣[1﹣(1﹣0.5×![]() )]×[2﹣(﹣3)2]﹣22
)]×[2﹣(﹣3)2]﹣22
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上表示整数的点称为整点,某数轴的单位长度为1cm,若在数轴上画出一条长2019cm的线段AB,则AB盖住的整点个数是( )
A.2019或2020B.2018或2019C.2019D.2020
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com