
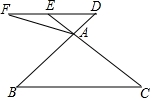
 如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF.
如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF.分析 (1)根据DE∥BC,得到△ADE∽△ABC,根据相似三角形的性质即可得到结论;
(2)由已知条件得到∠EAF=∠D,推出△FAE∽△FDA,根据相似三角形的性质即可得到结论.
解答 解:(1)∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{DE}{BC}$,
∵DE=6,
∴BC=9;
(2)∵∠FAE=∠B,∠B=∠D,
∴∠EAF=∠D,
∵∠F=∠F,
∴△FAE∽△FDA,
∴$\frac{EF}{FA}=\frac{FA}{DF}$,
∴DF=$\frac{F{A}^{2}}{EF}$=9.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 3(x+1)2=2(x-1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | x2+2x=x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
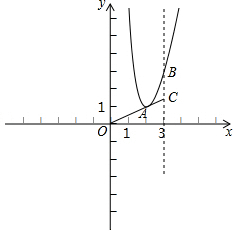 如图,在平面直角坐标系内,抛物线y=2x2+bx+c的顶点为A(2,1),同时与直线x=3交于点B,连接OA并延长与直线x=3交于点C.
如图,在平面直角坐标系内,抛物线y=2x2+bx+c的顶点为A(2,1),同时与直线x=3交于点B,连接OA并延长与直线x=3交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
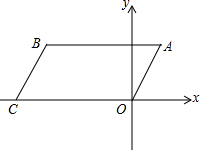 如图,四边形ABCO是平行四边形,点C在x轴的负半轴上,AO=2cm,AB=4cm,∠BAO=60°,将?ABCO绕点A逆时针旋转60°,得到对应的?ADEF,解答下列问题:
如图,四边形ABCO是平行四边形,点C在x轴的负半轴上,AO=2cm,AB=4cm,∠BAO=60°,将?ABCO绕点A逆时针旋转60°,得到对应的?ADEF,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
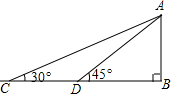 如图,某数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端点A的仰角为30°,再向旗杆的方向前进12米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端点A的仰角为45°,请计算旗杆AB的高度.(结果保留根号)
如图,某数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端点A的仰角为30°,再向旗杆的方向前进12米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端点A的仰角为45°,请计算旗杆AB的高度.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com