练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．下列方程中，关于x的一元二次方程是（　　）
    A．3（x+1）2=2（x-1）B．$\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0C．ax2+bx+c=0D．x2+2x=x2

    分析 依据一元二次方程的定义判断即可．

    解答 解：A、3（x+1）2=2（x-1）是一元二次方程，故A正确；
    B、$\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0是分式方程，故B错误；
    C、当a=0时，方程ax2+bx+c=0不是一元二次方程，故C错误；
    D、x2+2x=x2，整理得2x=0是一元一次方程，故D错误．
    故选：A．

    点评 本题主要考查的是一元二次方程的定义，掌握一元二次方程的定义是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    3．在△ABC中，若AB：BC：AC=3：4：5，则△ABC一定是（　　）
    A．锐角三角形B．钝角三角形C．直角三角形D．任意三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

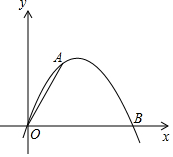    4．如图，已知二次函数y=ax2+bx的图象经过点A（2，4）和B（6，0）．
    （1）求a，b的值；
    （2）求该二次函数的图象的顶点坐标；
    （3）C是该二次函数的图象上A，B两点之间的一个动点，点C的横坐标为x，写出四边形OBCA的面积S关于点C的横坐标x的函数解析式，并求出S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．若“！”是一种数学运算符号，并1！=1，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1=24，…，则$\frac{50！}{48！}$的值为（　　）
    A．0.2！B．2450C．$\frac{25}{24}$D．49！

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．3的平方根是$±\sqrt{3}$；写出一个比-2小的无理数-$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．某地区修建一条长为6千米的公路．设每天的修建费为y（万元），修建天数为x天，当30≤x≤120时，y与x具有一次函数的关系，如表所示：
     x/万元 30 80120 
     y/万元 44n  26
    （I）求y关于x（30≤x≤120）的函数解析式和n的值．
    （Ⅱ）后来在修建的过程中计划发生改变，决定多修2千米，因此在没有增减建设力量的情况下，修完这条路比计划晚了15天，求原计划每天的修建费．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．当k=5时，关于x的方程4x2-（k+3）x+k=1有两个相等的实数根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，在平面直角坐标系中，点P从原点O出发．沿x轴向右以每秒一个单位长的速度运动t秒（t＞0），抛物线y=-x2+bx+c经过点O和点P．
    （1）求c．b（用t的代数式表示）：
    （2）抛物线y=-x2+bx+c与直线x=1和x=5分别交于M、N两点，当t＞1时，
    ①在点P的运动过程中，你认为sin∠MPO的大小是否会变化？若变化，说明理由；若不变，求出sin∠MPO的值：
    ②是否存在这样的/值，使得MP∥ON？如果存在，求出t值：如果不存在，请说明理由：
    （3）横、纵坐标都是整数的点叫做整点，若抛物线在点O，P之间的部分与线段OP所围成的区域内（包括边界）恰有5个整点，结合函数的图象，直接写出t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

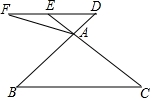    3．如图，在△ABC中，点D是BA边延长线上一点，过点D作DE∥BC，交CA延长线于点E，点F是DE延长线上一点，连接AF．
    （1）如果$\frac{AD}{AB}$=$\frac{2}{3}$，DE=6，求边BC的长；
    （2）如果∠FAE=∠B，FA=6，FE=4，求DF的长．

    查看答案和解析>>

    同步练习册答案