
【题目】(1)问题发现:如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD与CF的数量关系是 ;BD与CF位置关系是 .
(2)拓展探究:如图2,当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(3)解决问题:如图3,当△ABC绕点A逆时针旋转45°时,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,则线段DH的长为 .
时,则线段DH的长为 .

【答案】(1)BD=CF,BD⊥CF;(2)BD=CF成立,理由详见解析;(3)①详见解析;②DH=![]() .
.
【解析】
(1)易知,BD=CF,BD⊥CF;(2)先用“SAS”证明△CAF≌△BAD,再用全等三角形的性质即可得BD=CF成立;(3)利用△HFN与△AND的内角和以及它们的等角,得到∠NHF=90°,即可得①的结论;连接DF,延长AB,与DF交于点M,利用△BMD∽△FHD求解.
(1)易知,BD=CF,BD⊥CF,
故答案为:BD=CF,BD⊥CF;
(2)如图2中,BD=CF成立.

理由:由旋转得:AC=AB,∠CAF=∠BAD=θ;AF=AD,
在△ABD和△ACF中, ,
,
∴△ABD≌△ACF,
∴BD=CF.
(3)①证明:如图3中,

由(1)得,△ABD≌△ACF,
∴∠HFN=∠ADN,
∵∠HNF=∠AND,∠AND+∠AND=90°
∴∠HFN+∠HNF=90°
∴∠NHF=90°,
∴HD⊥HF,即BD⊥CF.
②如图4中,连接DF,延长AB,与DF交于点M.
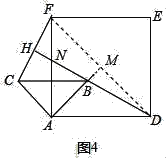
∵四边形ADEF是正方形,
∴∠MDA=45°,
∵∠MAD=45°
∴∠MAD=∠MDA,∠AMD=90°,
∴AM=DM,
∵AD=3![]() ,
,
在△MAD中,AM2+DM2=AD2,
∴AM=DM=3,
∴MB=AM﹣AB=3﹣2=1,
在Rt△BMD中,BM2+DM2=BD2,
∴BD=![]() =
=![]() .
.
在Rt△ADF中,AD=3![]() ,
,
∴DF=![]() AD=6,
AD=6,
由②知,HD⊥HF,
∴∠DHF=∠DMB=90°,
∵∠BDM=∠FDH,
∴△BDM∽△FDH,
∴![]() ,
,
∴DH=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.
(1)求证:四边形BEDF是菱形;
(2)若正方形ABCD的边长为4,AE=![]() ,求菱形BEDF的面积.
,求菱形BEDF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
问题:已知方程x2+x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=![]() ,把x=
,把x=![]() ,代入已知方程,
,代入已知方程,
得(![]() )2 +
)2 +![]() ﹣1=0.
﹣1=0.
化简,得y2+2y﹣4=0,
故所求方程为y2+2y﹣4=0
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):
(1)已知方程x2+2x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为 ;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,D是AB的中点,过点B作∠CBE=∠A,BE与射线CA相交于点E,与射线CD相交于点F.
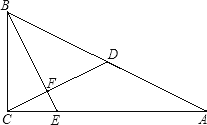
(1)如图,当点E在线段CA上时,求证:BE⊥CD;
(2)若BE=CD,那么线段AC与BC之间具有怎样的数量关系?并证明你所得到的结论;
(3)若△BDF是等腰三角形,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店老板在武汉发现一款羽绒服,预测能畅销市场,就用a万元购进了x件.这款羽绒服面市后,果然十分畅销,很快售完.于是老板又在上海购进了同款羽绒服,所购数量比在武汉所购的数量多20%,单价贵20元,总进货款比前一次多23%.
(1)请用含a和x的代数式分别表示在武汉以及上海购进的羽绒服的单价(单位:元/件);
(2)若服装店老板两次进货共花费17.84万元,在销售这款羽绒服时每件定价都是 1200元,第二次销售后期由于天气转暖,服装还剩![]() 没有卖出,老板决定打8折销售,最后全部售完.两次销售,服装店老板共盈利多少元?
没有卖出,老板决定打8折销售,最后全部售完.两次销售,服装店老板共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 过原点和点
过原点和点![]() ,位于第一象限的
,位于第一象限的![]() 点在直线
点在直线![]() 上,
上,![]() 轴上有一点
轴上有一点![]() ,
,![]() ,
,![]() 轴于点
轴于点![]() .
.
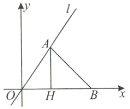
(1)求直线![]() 的解析式;
的解析式;
(2)求线段![]() 、
、![]() 的长度;
的长度;
(3)求![]() 点的坐标;
点的坐标;
(4)若![]() 点是线段
点是线段![]() 上一点,令
上一点,令![]() 长为
长为![]() ,
,![]() 的面积为
的面积为![]() .
.
①写出![]() 与
与![]() 的函数关系式,并指出自变量
的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
②当![]() 取何值时,
取何值时,![]() 为钝角三角形.
为钝角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ADB=∠ACB=90°,AC与BD相交于点O,且OA=OB,下列结论:①AD=BC;②AC=BD;③∠CDA=∠DCB;④CD∥AB,其中正确的有( )
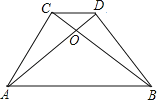
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某地火车站及周围的简单平面图.(每个小正方形的边长代表1千米.)
(1)请以火车站所在的位置为坐标原点,建立平面直角坐标系,并表示出体育场A、超市B市场C、文化宫D的坐标.
(2)在这个坐标平面内,连接OA,若∠AOB的度数大约为53°,请利用所给数据描述体育场相对于火车站的位置.
(3)要想用第(2)问的方法描述文化宫在火车站的什么位置,需要测量哪些数据?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com