
分析 (1)根据题意可以得到当整数x为何整数时,分式$\frac{2}{x+1}$的值也是整数;
(2)先化简题目中的代数式,可以发现与(1)的关系,从而可以解答本题.
解答 解:(1)若分式$\frac{2}{x+1}$的值也是整数,
则x+1=±1或x+1=±2,
解得,x1=0,x2=-2,x3=1,x4=-3,
即当x为0、-2、1或3时,分式$\frac{2}{x+1}$的值也是整数;
(2)$\frac{x+4}{x+1}$-$\frac{x-1}{x}$÷$\frac{{{x^2}-1}}{{{x^2}+2x}}$
=$\frac{x+4}{x+1}-\frac{x-1}{x}×\frac{x(x+2)}{(x+1)(x-1)}$
=$\frac{x+4}{x+1}-\frac{x+2}{x+1}$
=$\frac{2}{x+1}$,
由(1)知当x为0、-2、1或3时,分式$\frac{2}{x+1}$的值也是整数,
故当x为0、-2、1或3时,代数式$\frac{x+4}{x+1}$-$\frac{x-1}{x}$÷$\frac{{{x^2}-1}}{{{x^2}+2x}}$的值也是整数.
点评 本题考查分式的混合运算、分式的值,解答本题的关键是明确分式混合运算的计算方法,会求分式的值.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
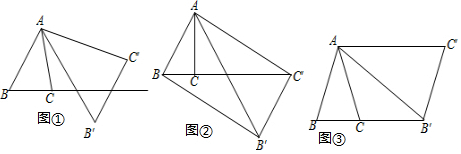
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
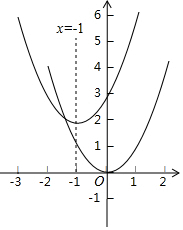 在学完《二次函数》后,老师给小明布置了家庭作业:完成下列表格,再用描点法在同一坐标系中画出y1与y2的函数图象.
在学完《二次函数》后,老师给小明布置了家庭作业:完成下列表格,再用描点法在同一坐标系中画出y1与y2的函数图象.| x | … | 0 | 1 | 2 |
| y1=ax2 | … | 0 | 1 | 4 |
| y2=ax2+bx+c | … | 3 | 6 | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
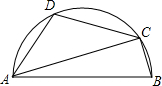 如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,$\widehat{AD}$=$\widehat{CD}$,求:∠BCD的度数.
如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,$\widehat{AD}$=$\widehat{CD}$,求:∠BCD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
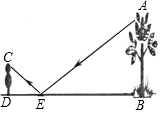 如图,王华把一面很小的镜子水平放置在离树底(点B)8米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢(点A),已知DE=4米,王华目高CD=1.6米,则树的高度AB为( )
如图,王华把一面很小的镜子水平放置在离树底(点B)8米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢(点A),已知DE=4米,王华目高CD=1.6米,则树的高度AB为( )| A. | 4.8米 | B. | 3.2米 | C. | 8米 | D. | 20米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com